Ecuația propagării căldurii

Reprezentare animată a evoluției temperaturii într-o placă metalică pătrată, așa cum prezice ecuația căldurii. Înălțimea și culoarea indică temperatura în fiecare punct. Starea inițială are o regiune uniform de caldă în formă de copită (cu roșu) înconjurată de o regiune uniform de rece (cu galben). Pe măsură ce trece timpul, căldura se difuzează în regiunea rece.

{{#invoke:Sidebar |collapsible | bodyclass = plainlist | titlestyle = padding-bottom:0.3em;border-bottom:1px solid #aaa; | title = Termodinamică | imagestyle = display:block;margin:0.3em 0 0.4em; | image = | caption = Schema unei mașini termice Carnot | listtitlestyle = text-align:center; | expanded = ecuații

| list1name = ramuri | list1title = Ramuri | list1 = Format:Flatlist

• Clasică
• Statistică
• Chimică
• Cuantică

• de echilibruFormat:\de neechilibru

| list2name = principii | list2title = Principii | list2 = Format:Flatlist

• Zero
• Primul
• Al doilea
• Al treilea

| list3name = sisteme | list3title = Sisteme | list3 = Format:Flatlist

• Izolat
• Închis
• Deschis
• Adiabatic

Format:Sidebar

| list4name = proprietăți | list4title = Propertăți ale sistemelor

| list4 =

Notă: Parametri conjugați cu italice

Format:Sidebar

| list5name = material | list5title = Proprietăți ale materialelor | list5 =

Capacitate termică masică	$c=$	$T$ $\partial S$ $N$ $\partial T$
Coeficient de compresibilitate	$\beta =-$	$1$ $\partial V$ $V$ $\partial p$
Coeficient de dilatare volumică	$\alpha =$	$1$ $\partial V$ $V$ $\partial T$

| list6name = ecuații | list6title = Ecuații | list6 = Format:Flatlist

• Teorema lui Carnot
• Teorema lui Clausius
• Relația fundamentală
• Ecuația căldurii
• Legile gazelor
  • ideale
• Stări corespondente

• Relațiile Maxwell
• Relațiile Onsager
• Ecuațiile Bridgman

• Tabel cu ecuații termodinamice

| list7name = potențiale | list7title = Potențiale | list7 = Format:Unbulleted list Format:Flatlist

• Entropie liberă

| list8name = istorie | list8title = Format:Hlist | list8 =

Format:Sidebar

| list9name = personalități | list9title = Personalități | list9 = Format:Flatlist

• Bernoulli
• Boltzmann
• Bridgman
• Carathéodory
• Carnot
• Clapeyron
• Clausius
• de Donder
• Duhem
• Gibbs
• von Helmholtz
• Joule
• Kelvin
• Lewis
• Massieu
• Maxwell
• von Mayer
• Nernst
• Onsager
• Planck
• Rankine
• Smeaton
• Stahl
• Tait
• Thompson
• van der Waals
• Waterston

Format:Endflatlist | below =

• Categorie

}}

În matematică și fizică ecuația propagării căldurii (pe scurt ecuația căldurii) este o ecuație cu derivate parțiale parabolică. Teoria ecuației căldurii a fost dezvoltată pentru prima dată de Joseph Fourier în 1822 cu scopul de a modela modul în care o cantitate precum căldura difuzează printr-o zonă dată. De atunci, ecuația căldurii și variantele sale s-au dovedit a fi fundamentale în multe părți ale matematicii pure și aplicate.

Definiție

Fie o submulțime deschisă Format:Mvar din Format:Math și un subinterval Format:Mvar din Format:Math, se spune că o funcție Format:Math este o soluție a ecuației căldurii dacă:

$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x_1^2}+\cdots +\frac{{\partial }^{2}u}{\partial x_n^2},$

unde Format:Math este un punct general din domeniu. De obicet Format:Mvar reprezintă timpul, iar Format:Math sunt variabile spațiale, chiar și în contexte abstracte, în care aceste cuvinte nu au un sens intuitiv. Colecția de variabile spațiale este adesea denumită simplu Format:Mvar. Pentru orice valoare dată a lui Format:Mvar, membrul drept al ecuației este laplacianul funcției Format:Math. Ca atare, ecuația căldurii este adesea scrisă mai compact ca

$\frac{\partial u}{\partial t}=\mathrm{\Delta }u$

În contexte de fizică și inginerie, în special în contextul difuziunii printr-un mediu, este uzual să se fixeze un sistem de coordonate carteziene și apoi să se ia în considerare cazul specific al unei funcții Format:Math de trei variabile spațiale Format:Math și variabila de timp Format:Mvar. Se spune atunci că Format:Mvar este o soluție a ecuației căldurii dacă

$\frac{\partial u}{\partial t}=\alpha (\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2})$

în care Format:Math este un coeficient pozitiv, numit difuzivitatea termică a mediului. Pe lângă alte fenomene fizice, această ecuație descrie fluxul de căldură într-un mediu omogen și izotrop, cu Format:Math fiind temperatura în punctul Format:Math și timpul Format:Mvar. Dacă mediul nu este omogen și izotrop, atunci Format:Mvar nu ar fi un coeficient fix, ci ar depinde de Format:Math; ecuația ar avea și o formă puțin diferită. În bibliografia de fizică și inginerie, se obișnuiește ca laplacianul să fie notat Format:Math în loc de Format:Math.

În matematică, fizică și inginerie se obișnuiește să se folosească notația lui Newton pentru derivatele timpului, astfel încât $\dot{u}$ este folosit pentru a desemna Format:Math, deci ecuația poate fi scrisă

$\dot{u}=\mathrm{\Delta }u$

De reținut că posibilitatea de a folosi fie Format:Math fie Format:Math pentru a desemna laplacianul, fără referire explicită la variabilele spațiale, este o reflectare a faptului că laplacianul este independent de alegerea sistemului de coordonate. În termeni matematici, s-ar spune că laplacianul este invariant translațional și rotațional. De fapt, este (vorbind vag) cel mai simplu operator diferențial care are aceste simetrii. Aceasta poate fi considerată o justificare semnificativă (și pur matematică) a utilizării laplacianului și a ecuației căldurii în modelarea oricăror fenomene fizice omogene și izotrope, din care difuzia căldurii este un exemplu principal.

Constanta de difuzivitate, Format:Mvar, adesea nu este prezentă în studiile matematice ale ecuației căldurii, în timp ce valoarea acesteia poate fi foarte importantă în inginerie. Aceasta nu este o diferență majoră, din următorul motiv. Fie Format:Mvar o funcție cu

$\frac{\partial u}{\partial t}=\alpha \mathrm{\Delta }u.$

Se definește o nouă funcție, $v(t,x)=u(t/\alpha ,x)$. Apoi, conform regulii de derivare a funcțiilor compuse, se obține

$\frac{\partial }{\partial t}v(t,x)=\frac{\partial }{\partial t}u(t/\alpha ,x)={\alpha }^{-1}\frac{\partial u}{\partial t}(t/\alpha ,x)=\mathrm{\Delta }u(t/\alpha ,x)=\mathrm{\Delta }v(t,x)$

Astfel, există o modalitate simplă de echivalare între soluțiile ecuației căldurii cu o valoare generală Format:Mvar și soluțiile ecuației căldurii cu Format:Math. Ca atare, de dragul analizei matematice, este adesea suficient să se ia în considerare doar cazul Format:Math.

Deoarece $\alpha >0$ există o altă opțiune pentru a defini un $v$ care să satisfacă $\frac{\partial }{\partial t}v=\mathrm{\Delta }v$ ca în relațiile de mai sus punând $v(t,x)=u(t,{\alpha }^{1/2}x)$. De reținut că cele două mijloace posibile de definire a noii funcții $v$ discutate aici înseamnă, în termeni fizici, schimbarea unității de măsură a timpului sau a unității de măsură a lungimii.

Ecuația pentru o stare staționară

În regim de echilibru, ecuația căldurii nu este, prin definiție, dependentă de timp. Cu alte cuvinte, se presupune că există condiții astfel încât:

$\frac{\partial u}{\partial t}=0$

Această condiție depinde de constanta de timp și de timpul trecut de când au fost impuse condițiile de limită. Astfel, condiția este îndeplinită în situațiile în care „constanta de echilibru de timp este suficient de rapidă” încât ecuația mai complexă a căldurii dependentă de timp să poată fi aproximată prin cazul regimului staționar. Echivalent, starea de echilibru există pentru toate cazurile în care „a trecut suficient timp” încât câmpul termic Format:Mvar nu mai evoluează în timp.

În cazul regimului staționar, un gradient termic spațial poate sau nu exista, dar dacă există, nu se schimbă în timp. Prin urmare, această ecuație descrie rezultatul final al tuturor problemelor termice în care o sursă este pornită (de exemplu, un motor pornit) și a trecut suficient timp pentru ca toți gradienții permanenți de temperatură să se stabilizeze în spațiu, după care aceste pante nu se mai schimbă în timp (de exemplu un motor care a functionat suficient de mult). Cealaltă soluție (trivială) este ca toți gradienții spațiali de temperatură să se anuleze, caz în care temperatura devine uniformă și în spațiu.

Ecuația este mult mai simplă și poate ajuta la înțelegerea mai bună a fizicii materialelor fără a se concentra pe dinamica procesului de transmitere a căldurii. Este utilizat pe scară largă pentru probleme simple de inginerie presupunând că există un echilibru al câmpurilor de temperatură și al transmiterii căldurii în timp.

Stare de echilibru:

$\frac{\partial u}{\partial t}=0$

Ecuația căldurii în regim de echilibru pentru un volum care conține o sursă de căldură (cazul neomogen), este ecuația lui Poisson:

$-\lambda {\mathrm{\nabla }}^{2}u=q$

unde Format:Mvar este temperatura, Format:Mvar este conductivitatea termică iar Format:Mvar este rata de generare a căldurii pe unitatea de volum.

În electrostatică, acest lucru este echivalent cu cazul în care spațiul în cauză conține o sarcină electrică.

Ecuația căldurii în stare staționară fără o sursă de căldură în volum (cazul omogen) este la fel cu ecuația din electrostatică pentru un volum de spațiu liber care nu conține o sarcină. Cazul este descris de ecuația lui Laplace:

${\mathrm{\nabla }}^{2}u=0$

Interpretare

Informal, operatorul laplacian Format:Math dă diferența dintre valoarea medie a unei funcții în vecinătatea unui punct și valoarea acesteia în acel punct. Astfel, dacă Format:Mvar este temperatura, Format:Math indică dacă (și cât de mult) materialul din jurul fiecărui punct este, în medie, mai cald sau mai rece decât materialul din acel punct.

Conform principiului al doilea al termodinamicii, căldura va trece de la corpurile mai calde către corpurile mai reci adiacente, proporțional cu diferența de temperatură și cu conductivitatea termică a materialului dintre ele. Când căldura trece într-un (respectiv, dintr-un) material, temperatura acestuia crește (respectiv, scade), proporțional cu raportul dintre cantitatea de căldură și cantitatea de material (masă), raport numit capacitatea termică masică a materialului.

Prin combinarea acestor observații, ecuația căldurii spune că viteza $\dot{u}$ cu care materialul într-un punct se va încălzi (sau se va răci) este proporțională cu cât de mult mai cald (sau mai rece) este mediul înconjurător al materialului. Coeficientul Format:Mvar din ecuație ia în considerare conductivitatea termică, capacitatea termică masică și densitatea materialului.

Interpretarea ecuației

Prima jumătate a descrierii fizice de mai sus poate fi pusă într-o formă matematică. Pentru orice Format:Mvar fix, există

$\begin{array}{cc}{u}_{(x)}(0)& =u(x)\\ u_{{(}^{\prime }x)}(0)& =0\\ u_{{(}^{″}x)}(0)& =\frac{1}{n}\mathrm{\Delta }u(x)\end{array}$

unde Format:Math este o funcție de o singură variabilă care arată valoarea medie a lui Format:Mvar pe o suprafață sferică cu raza Format:Mvar și centrul în Format:Mvar; ea poate fi definită prin

$u_{(x)}(r)=\frac{1}{{\omega }_{n-1}{r}^{n-1}}\underset{\{y:|x-y|=r\}}{\int }ud{\mathscr{H}}^{n-1},$

unde cu Format:Math este notată aria suprafeței unei bile unitate din spațiul euclidian Format:Mvar-dimensional. Aceasta formalizează afirmația de mai sus că valoarea lui Format:Math într-un punct Format:Mvar măsoară diferența dintre valoarea lui Format:Math și valoarea lui Format:Mvar în punctele apropiate de Format:Mvar, în sensul că acesta din urmă este definit de valorile lui Format:Math pentru valori pozitive mici ale lui Format:Mvar.

În urma acestei observații, se poate interpreta ecuația căldurii ca impunând o „mediere infinitezimală” a unei funcții. Fiind dată o soluție a ecuației căldurii, valoarea lui Format:Math pentru o mică valoare pozitivă a Format:Math poate fi aproximată ca produsul dintre Format:Math și valoarea medie a funcției Format:Math peste o sferă cu rază foarte mică, cu centrul în Format:Mvar.

Caracterul soluțiilor

Rezolvarea unei ecuații a călduri într-un spațiu unidimensional. Temperatura ($u$) este distribuită inițial pe un interval unidimensional, lung de o unitate (x= [0,1]) cu puncte de la capete izolate. Distribuția se apropie de echilibru în timp.

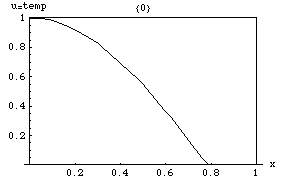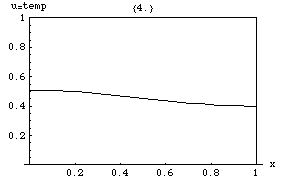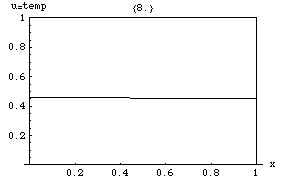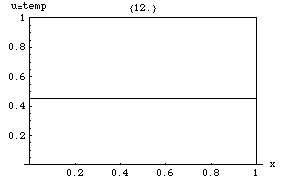
Ecuația căldurii implică faptul că vârfurile (maxime locale) ale $u$ vor fi erodate treptat, în timp ce depresiunile (minime locale) vor fi umplute. Valoarea la un moment dat va rămâne stabilă doar atâta timp cât este egală cu valoarea medie din împrejurimile sale imediate. În special, dacă valorile dintr-o vecinătate sunt foarte apropiate de o funcție liniară $Ax+By+Cz+D$, atunci valoarea din centrul acelei vecinătăți nu se va schimba în acel moment. (adică derivata $\dot{u}$ se va anula).

O consecință mai subtilă este Format:Ill-wd, care spune că valoarea maximă a lui $u$ în orice regiune $R$ a mediului nu va depăși valoarea maximă care anterior a apărut în $R$, cu excepția cazului în care se află la limita lui $R$. Adică, temperatura maximă într-o regiune $R$ poate crește numai dacă căldura intră din exteriorul $R$. Aceasta este o proprietate a ecuațiilor diferențiale parțiale parabolice și nu este dificil de demonstrat matematic.

O altă proprietate interesantă este că, chiar dacă $u$ are inițial un salt ascuțit (discontinuitate) a valorilor pe o suprafață din interiorul mediului, saltul este imediat netezit de o rată de transfer momentană, infinitezimal de scurtă, dar infinit de mare de căldură prin acea suprafață. De exemplu, dacă două corpuri izolate, inițial la temperaturi uniforme, dar diferite, $u_0$ și $u_1$, sunt făcute să se atingă, temperatura la punctul de contact va prelua imediat ceva valoare intermediară și o zonă se va dezvolta în jurul acestui punct în care $u$ va varia treptat între $u_0$ și $u_1$.

Dacă o anumită cantitate de căldură este aplicată brusc într-un punct din mediu, aceasta se va răspândi în toate direcțiile sub forma unei unde de difuzie. Spre deosebire de undele elastice și cele electromagnetice, viteza unei unde de difuzie scade cu timpul: pe măsură ce se răspândește pe o regiune mai mare, gradientul de temperatură scade, prin urmare fluxul de căldură scade și el.

Exemple

Transmiterea căldurii într-o bară uniformă

Pentru fluxul de căldură, ecuația căldurii decurge din legile fizice a conducției termice și a conservării energiei.

Dn legea lui Fourier pentru un mediu izotrop, rata de transfer printr-o suprafață a energiei termice pe unitate de suprafață este proporțională cu gradientul de temperatură negativ transversal pe ea:

$𝐪=-\lambda \mathrm{\nabla }u$

unde $\lambda$ este conductivitatea termică a materialului, $u=u(𝐱,t)$ este temperatura, iar $𝐪=𝐪(𝐱,t)$ este câmpul vectorial care indică mărimea și direcția fluxului termic în punctul $𝐱$ din spațiu și la momentul $t$.

Dacă mediul este o tijă subțire din material uniform și cu secțiune constantă, poziția Format:Mvar este o singură coordonată și fluxul termic $q=q(t,x)$ în direcția $x$ este un câmp scalar. Ecuația devine:

$q=-\lambda \frac{\partial u}{\partial x}$

Fie $Q=Q(x,t)$ energia internă (căldura) per unitate de volum a barei în funcție de poziția punctului și de momentul de timp. Fluxul termic din material pe unitatea de volum, $\partial Q/\partial t,$ este proporțional cu viteza de modificare a temperaturii sale, $\partial u/\partial t,$ adică

$\frac{\partial Q}{\partial t}=c\rho \frac{\partial u}{\partial t}$

unde $c$ este capacitatea termică masică (în cazul gazelor la presiune constantă) iar $\rho$ este densitatea materialului. Această formă presupune că densitatea și capacitatea termică masică sunt constante în spațiu și timp.

Aplicând legea conservării energiei unui element mic al mediului, centrat pe $x$, se ajunge la concluzia că viteza cu care căldura se propagă într-un punct dat $x$ este egală cu derivata fluxului termic în acel punct (diferența dintre fluxurile termice de fiecare parte a particulei), adică

$\frac{\partial Q}{\partial t}=-\frac{\partial q}{\partial x}$

Din ecuațiile de mai sus rezultă că

$\frac{\partial u}{\partial t}=-\frac{1}{c\rho }\frac{\partial q}{\partial x}=-\frac{1}{c\rho }\frac{\partial }{\partial x}(-\lambda \frac{\partial u}{\partial x})=\frac{\lambda }{c\rho }\frac{{\partial }^{2}u}{\partial x^2}$

care este ecuația unidimensională a căldurii, cu coeficientul de difuzivitate

$\alpha =\frac{\lambda }{c\rho }$

Această cantitate se numește difuzivitatea termică a mediului.

Luarea în considerare a pierderilor radiative

Un termen suplimentar poate fi introdus în ecuație pentru a lua în considerare pierderea de căldură prin radiație. Conform legii Stefan–Boltzmann, acest termen este $\mu (u^4-v^4)$, unde $v=v(x,t)$ este temperatura mediului înconjurător, iar $\mu$ este un coeficient care depinde de constanta Stefan–Boltzmann și de emisivitatea materialului. Rata de schimbare a energiei interne devine

$\frac{\partial Q}{\partial t}=-\frac{\partial q}{\partial x}-\mu (u^4-v^4)$

iar ecuația pentru evoluția lui $u$ devine

$\frac{\partial u}{\partial t}=\frac{\lambda }{c\rho }\frac{{\partial }^{2}u}{\partial x^2}-\frac{\mu }{c\rho }(u^4-v^4).$

Mediu izotrop neuniform

De reținut că ecuația de stare, dată de principiul întâi al termodinamicii (adică conservarea energiei), este scrisă în următoarea formă (presupunând că nu există transfer de masă sau schimb de energie prin radiație). Această formă este mai generală și mai utilă pentru a recunoaște care termen este influențat de care proprietate (de exemplu, de c_p sau de $\rho$).

$\rho c_p\frac{\partial T}{\partial t}-\mathrm{\nabla }\cdot \left(\lambda \mathrm{\nabla }T\right)={\dot{q}}_V$

unde ${\dot{q}}_V$ este sursa de căldură volumică.

Flux termic în medii anizotrope neomogene

În general, studiul transmiterii căldurii prin conducție se bazează pe mai multe principii. Fluxul termic este o formă de flux de energie, ca atare este semnificativ să vorbim despre viteza fluxului termic într-o regiune a spațiului.

• Viteza fluxului de căldură într-o regiune Format:Mvar este dată de o cantitate dependentă de timp Format:Math. Fie Format:Mvar densitatea lui Format:Mvar astfel încât

$q_t(V)=\underset{V}{\int }Q(x,t)dx$

• Fluxul termic este o funcție vectorială dependentă de timp Format:Math caracterizată după cum urmează: viteza căldurii care trece printr-un element de suprafață infinitezimal cu aria Format:Mvar și cu versorul normal Format:Math este

$𝐇(x)\cdot 𝐧(x)dS.$

Astfel, fluxul termic prin Format:Mvar este dat și de integrala de suprafață

$q_t(V)=-\underset{\partial V}{\int }𝐇(x)\cdot 𝐧(x)dS$

unde Format:Math este versorul normal orientat spre exterior în Format:Mvar.

• Legea lui Fourier afirmă că fluxul termic are următoarea dependență liniară de gradientul de temperatură

$𝐇(x)=-𝐀(x)\cdot \mathrm{\nabla }u(x)$

unde Format:Math este o matrice reală 3 × 3 simetrică și pozitiv definită.

• Cu Format:Ill-wd, integrala de suprafață anterioară pentru fluxul de căldură prin Format:Mvar poate fi transformată în integrala de volum

$\begin{array}{cc}{q}_t(V)& =-\underset{\partial V}{\int }𝐇(x)\cdot 𝐧(x)dS\\ & =\underset{\partial V}{\int }𝐀(x)\cdot \mathrm{\nabla }u(x)\cdot 𝐧(x)dS\\ & =\underset{V}{\int }\sum _{i,j}{\partial }_{x_i}(a_{ij}(x){\partial }_{x_j}u(x,t))dx\end{array}$

• Viteza schimbării temperaturii în Format:Mvar este proporțională cu căldura care trece printr-un element de volum infinitezimal, unde constanta de proporționalitate este dependentă de o constantă κ

$${\partial }_{t}u(x,t)=\kappa (x)Q(x,t)$$

Combinând aceste ecuații, rezultă ecuația generală a fluxului termic:

${\partial }_{t}u(x,t)=\kappa (x)\sum _{i,j}{\partial }_{x_i}(a_{ij}(x){\partial }_{x_j}u(x,t))$

Note

• Coeficientul Format:Math este inversul produsului dintre capacitatea termică masică a substanței și în Format:Mvar și densitatea ei în Format:Mvar:

$\kappa =1/(\rho c_p)$.

• În cazul unui mediu izotrop, matricea Format:Math este o matrice scalară egală cu conductivitatea termică Format:Mvar.
• În cazul anizotrop în care matricea coeficienților Format:Math nu este scalară și/sau dacă depinde de Format:Mvar, atunci o formulă explicită pentru soluția ecuației căldurii poate fi rar scrisă, deși de obicei este posibil să se ia în considerare problema Cauchy abstractă asociată și să se arate că este o Format:Ill-wd și/sau să se arate unele proprietăți calitative (cum ar fi conservarea datelor inițiale pozitive, viteza infinită a propagării, convergența către un echilibru, proprietăți de netezire). Acest lucru se face de obicei prin teoria Format:Ill-wd: de exemplu, dacă Format:Mvar este o matrice simetrică, atunci Format:Ill-wd definit de

$Au(x):=\sum _{i,j}{\partial }_{x_i}{a}_{ij}(x){\partial }_{x_j}u(x)$

este Format:Ill-wd și disipativ, astfel prin Format:Ill-wd generează un semigrup cu un parametru.

Problema tridimensională

În cazurile particulare de propagare a căldurii într-un mediu izotrop și omogen dintr-un spațiu tridimensional, această ecuație este

$\frac{\partial u}{\partial t}=\alpha {\mathrm{\nabla }}^{2}u=\alpha (\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2})=\alpha (u_{xx}+u_{yy}+u_{zz})$

unde $u=u(x,y,z,t)$ este temperatura în funcție de spațiu (poziție) și timp;

$\frac{\partial u}{\partial t}$ este viteza de variație a temperaturii într-un punct și în timp;

$u_{xx}$, $u_{yy}$ și $u_{zz}$ sunt derivatele parțiale spațiale de ordinul al doilea ale temperaturii în direcțiile $x,y,$ respectiv $z$;

$\alpha \equiv \frac{\lambda }{c_p\rho }$ este difuzivitatea termică, o proprietate de material care depinde de conductivitatea termică, $\lambda ,$ capacitatea termică masică, $c_p,$ și densitatea, $\rho ,$ ale materialului.

Dacă mediul nu este tot spațiul, pentru a rezolva ecuația căldurii în mod unic, trebuie specificate condițiile la limită pentru Format:Mvar. Pentru a determina unicitatea soluțiilor în întreg spațiul este necesar să se presupună condiții suplimentare, de exemplu o limită exponențială a creșterii soluțiilor sau o condiție de semn (soluțiile nenegative sunt unice prin rezultatul lui David Widder).

Soluțiile ecuației căldurii sunt caracterizate printr-o netezire treptată a distribuției inițiale a temperaturii ca urmare a fluxului de căldură din zonele mai calde spre cele mai reci ale unui obiect. În general, multe stări și condiții de pornire diferite vor tinde către același echilibru. În consecință, a inversa soluția și a concluziona ceva evoluțiile anterioare sau despre condițiile inițiale pe baza distribuției actuale a căldurii este ceva foarte inexact, cu excepția unor perioade de timp foarte scurte.

Ecuația căldurii este prototipul ecuațiilor cu derivate parțiale parabolice.

Folosind operatorul Laplace, ecuația căldurii poate fi simplificată și generalizată pentru ecuații similare din spații cu un număr arbitrar de dimensiuni, ca

$u_t=\alpha {\mathrm{\nabla }}^{2}u=\alpha \mathrm{\Delta }u,$

unde operatorul Laplace, Δ sau ∇², divergența gradientului, se aplică variabilelor spațiale.

Ecuația căldurii modelează difuzia căldurii, precum și alte procese difuzive, cum ar fi difuzia particulelor. Deși nu sunt de natură difuză, unele probleme de mecanică cuantică sunt, de asemenea, guvernate de un analog matematic al ecuației căldurii. De asemenea, poate fi folosit pentru a modela unele fenomene care apar în finanțe. Ecuația și diverși analogi neliniari au fost, de asemenea, utilizați în analiza imaginilor.

Din punct de vedere teoretic, ecuația căldurii încalcă teoria relativității restrânse, deoarece soluțiile sale implică propagarea instantanee a unei perturbații. Partea perturbației din afara Format:Ill-wd a viitorului poate fi de obicei neglijată în siguranță, dar dacă este necesar să se dezvolte o viteză rezonabilă pentru transmiterea căldurii, ar trebui să fie considerată în loc problemă hiperbolică sub forma unei ecuații cu derivate parțiale care conține o derivată de ordinul al doilea în funcție de timp. Unele modele de conducție neliniară a căldurii (care sunt și ecuații parabolice) au soluții cu viteză finită de transmitere a căldurii.

Generarea internă de căldură

Funcția Format:Mvar de mai sus reprezintă temperatura unui corp. Alternativ, uneori este convenabil să se schimbe unitățile și să se reprezinte Format:Mvar ca densitatea de căldură a unui mediu. Deoarece într-un mediu omogen densitatea căldurii este proporțională cu temperatura, ecuația căldurii este valabilă în noile unități.

Fie un corp în care este valabilă ecuația căldurii și, în plus, generează căldură pe unitatea de volum (de exemplu, în wați pe metru cub, W/m³) cu o rată dată de o funcție cunoscută Format:Mvar care variază în spațiu și timp. Atunci căldura pe unitatea de volum Format:Mvar satisface o ecuație

$\frac{1}{\alpha }\frac{\partial u}{\partial t}=(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial z^2})+\frac{1}{\lambda }q$

De exemplu, un filament de wolfram al unui bec incandescent generează căldură, deci ar avea o valoare pozitivă diferită de zero pentru Format:Mvar atunci când este pornit. În timp ce lumina este stinsă, valoarea lui Format:Mvar pentru filamentul de wolfram ar fi zero.

Rezolvarea ecuației căldurii folosind serii Fourier

Setare fizică idealizată pentru conducția termică într-o bară cu condiții la limită omogene

Următoarea tehnică de soluționare pentru ecuația căldurii a fost propusă de Joseph Fourier în tratatul său Théorie analytique de la chaleur (în Format:Ro), publicat în 1822. Fie ecuația căldurii pentru o variabilă spațială, de exemplu într-o bară. Ecuația este

$u_t=\alpha u_{xx}$

unde Format:Math este o funcție de două variabile Format:Mvar și Format:Mvar Format:Mvar este variabila spațială, deci Format:Math, unde Format:Mvar este lungimea barei, iar Format:Mvar este timpul, deci Format:Math

Fie condiția inițială

$u(x,0)=f(x)\mathrm{\forall }x\in [0,L]$

unde funcția Format:Mvar este dată, și condițiile la limită

$u(0,t)=0=u(L,t)\mathrm{\forall }t>0$

Se caută o soluție a ecuației care să nu fie zero peste tot, care să satisfacă condițiile la limită date, dar cu următoarea proprietate: Format:Mvar este un produs în care dependențele lui Format:Mvar de Format:Math sunt separate, adică:

$u(x,t)=X(x)T(t)$

Această tehnică de soluționare se numește separarea variabilelor. Înlocuind Format:Mvar înapoi în ecuația inițială

$\frac{T^{\prime }(t)}{\alpha T(t)}=\frac{X^{″}(x)}{X(x)}$

Deoarece membrul drept depinde doar de Format:Mvar, iar cel stîng doar de Format:Mvar, ambii membri sunt egali cu o valoare constantă Format:Mvar. Astfel:

$T^{\prime }(t)=-\varphi \alpha T(t)$

și

$X^{″}(x)=-\varphi X(x)$

Acum se va arăta că soluțiile netriviale ale acestei ecuații pentru valorile lui Format:Math nu pot apărea:

1. Fie Format:Math. Atunci există numerele reale Format:Mvar astfel încât $$X(x)=B{e}^{\sqrt{-\varphi }x}+C{e}^{-\sqrt{-\varphi }x}$$ Însă Format:Math și prin urmare Format:Math care arată că Format:Math peste tot.
2. Fie Format:Math Atunci există numerele reale Format:Mvar astfel încât Format:Math Prin urmare, analog, u Format:Math peste tot.
3. Deci, trebuie să fie Format:Math Atunci există numerele reale Format:Mvar astfel încât $$T(t)=A{e}^{-\varphi \alpha t}$$ și $$X(x)=B\sin \left(\sqrt{\varphi }x\right)+C\cos \left(\sqrt{\varphi }x\right)$$

În final se obține Format:Math și pentru unii întregi pozitivi Format:Mvar,

$\sqrt{\varphi }=n\frac{\pi }{L}$

Aceasta rezolvă ecuația căldurii pentru acest caz particular. Se poate arăta că soluția este

$u(x,t)=\sum _{n=1}^{\mathrm{\infty }}{D}_n\sin \left(\frac{n\pi x}{L}\right)e^{-\frac{n^2{\pi }^2\alpha t}{L^2}}$

unde

$D_n=\frac{2}{L}\underset{0}{\overset{L}{\int }}f(x)\sin \left(\frac{n\pi x}{L}\right)dx$

Generalizarea tehnicii de rezolvare

Tehnica de rezolvare folosită mai sus poate fi extinsă la multe alte tipuri de ecuații. Ideea este că operatorul Format:Mvar cu condițiile la limită zero poate fi reprezentat în termenii Format:Ill-wd. Acest lucru duce în mod natural la una dintre ideile de bază ale Format:Ill-wd a Format:Ill-wd liniari.

Fie operatorul liniar Format:Math Șirul infinit de funcții

$e_n(x)=\sqrt{\frac{2}{L}}\sin \left(\frac{n\pi x}{L}\right)$

pentru n ≥ 1 sunt funcții proprii ale lui Format:Math.Într-adevăr,

$\mathrm{\Delta }{e}_n=-\frac{n^2{\pi }^2}{L^2}{e}_n$

Mai mult, orice funcție proprie Format:Mvar a lui Format:Math cu condițiile la limită Format:Math are forma Format:Mvar pentru unele Format:Math Funcțiile Format:Mvar pentru Format:Math formează un șir ortonormal în raport cu un anumit spațiu prehilbertian pe spațiul funcțiilor reale pe [0, L]. Asta înseamnă că

$⟨e_n,e_m⟩=\underset{0}{\overset{L}{\int }}{e}_n(x)e_m^{*}(x)dx={\delta }_{mn}$

În cele din urmă, secvența Format:Math se întinde pe un subspațiu liniar dens de Format:Math. Aceasta arată că de fapt s-a diagonalizat operatorul Format:Math.

Proprietate a valorii medii

Soluțiile ecuației căldurii

$({\partial }_t-\mathrm{\Delta })u=0$

satisfac o proprietate a valorii medii analogă cu proprietățile valorilor medii ale funcțiilor armonice, soluții ale

$\mathrm{\Delta }u=0,$

dar ceva mai complicat. Exact, dacă Format:Mvar este o soluție a

$({\partial }_t-\mathrm{\Delta })u=0$

și

$(x,t)+E_{\varphi }\subset \mathrm{d}\mathrm{o}\mathrm{m}(u)$

atunci

$u(x,t)=\frac{\varphi }{4}\underset{E_{\varphi }}{\int }u(x-y,t-s)\frac{|y{|}^2}{s^2}dsdy,$

unde Format:Mvar este bila de căldură, adică este o mulțime de nivelul superior al soluției fundamentale a ecuației căldurii:

$E_{\varphi }:=\{(y,s):\mathrm{\Phi }(y,s)>\varphi \},$

$\mathrm{\Phi }(x,t):=(4t\pi {)}^{-\frac{n}{2}}\exp (-\frac{|x{|}^2}{4t})$

De reținut că

$\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{m}(E_{\varphi })=o(1)$

cum Format:Math formula de mai sus este valabilă pentru orice Format:Math din mulțimea (deschisă) Format:Math pentru Format:Mvar suficient de mare. (Invers, orice funcție Format:Mvar care satisface proprietatea valorii medii de mai sus pe un domeniu deschis din Format:Math este o soluție a ecuației căldurii.)

Soluții fundamentale

O soluție fundamentală a ecuației căldurii este o soluție care corespunde condiției inițiale a unei surse punctuale inițiale de căldură aflată într-o poziție cunoscută. Acestea pot fi folosite pentru a găsi o soluție generală a ecuației căldurii pe anumite domenii.

În unidimensional, Format:Ill-wd este o soluție a problemei valorii inițiale (prin Format:Ill-wd, echivalentă cu definiția funcției lui Green ca una cu o funcție delta ca soluție a primei ecuații)

$\{\begin{array}{cc}{u}_t(x,t)-\lambda u_{xx}(x,t)=0& (x,t)\in ℝ\times (0,\mathrm{\infty })\\ u(x,0)=\delta (x)& \end{array}$

unde $\delta$ este funcția lui Dirac. Soluția fundamentală la această problemă este dată de Format:Ill-wd

$\mathrm{\Phi }(x,t)=\frac{1}{\sqrt{4\pi \lambda t}}\exp (-\frac{x^2}{4\lambda t}).$

Se poate obține soluția generală a ecuației unidimensionale a căldurii cu condiția inițială Format:Math pentru Format:Math și Format:Mvar aplicând convoluția:

$u(x,t)=\int \mathrm{\Phi }(x-y,t)g(y)dy$

Pentru mai multe variabile spațiale soluția fundamentală rezolvă problema analoagă

$\{\begin{array}{cc}{u}_t(𝐱,t)-\lambda \sum _{i=1}^n{u}_{x_i{x}_i}(𝐱,t)=0& (𝐱,t)\in {ℝ}^n\times (0,\mathrm{\infty })\\ u(𝐱,0)=\delta (𝐱)\end{array}$

Soluția fundamentală în n-variabile este produsul soluțiilor fundamentale din fiecare variabilă; adică,

$\mathrm{\Phi }(𝐱,t)=\mathrm{\Phi }(x_1,t)\mathrm{\Phi }(x_2,t)\cdots \mathrm{\Phi }(x_n,t)=\frac{1}{\sqrt{(4\pi \lambda t{)}^n}}\exp (-\frac{𝐱\cdot 𝐱}{4\lambda t})$

Soluția generală a ecuației căldurii pe Format:Math se obține apoi printr-o convoluție, astfel încât să se rezolve problema valorii inițiale cu Format:Math obținându-se

$u(𝐱,t)=\underset{{ℝ}^n}{\int }\mathrm{\Phi }(𝐱-𝐲,t)g(𝐲)d𝐲$

Problema generală pe un domeniu Format:Math este

$\{\begin{array}{cc}{u}_t(𝐱,t)-\lambda \sum _{i=1}^n{u}_{x_i{x}_i}(𝐱,t)=0& (𝐱,t)\in \mathrm{\Omega }\times (0,\mathrm{\infty })\\ u(𝐱,0)=g(𝐱)& 𝐱\in \mathrm{\Omega }\end{array}$

cu condiții la limită fie de tip Dirichlet, fie de tip Neumann. O funcție Green există întotdeauna, dar dacă domeniul Format:Math nu poate fi descompus cu ușurință în probleme cu o singură variabilă, s-ar putea să nu fie posibil să fie scrisă explicit. Alte metode pentru obținerea funcțiilor Green sunt Format:Ill-wd, separarea variabilelor și transformata Laplace.

Unele soluții ale funcției lui Green în spațiul unidimensional

Green's Function Library conține o varietate de soluții fundamentale pentru ecuația căldurii. În unele dintre acestea, domeniul spațial este (−∞,∞). În altele, este intervalul (0,∞) cu condiții la limită fie de tip Neumann, fie de tip Dirichlet. Un alt tip este că unele dintre acestea rezolvă ecuația neomogenă

$u_t=k{u}_{xx}+f.$

inde Format:Mvar este o funcție dată de Format:Mvar și Format:Mvar.

Ecuația căldurii omogenă

Problema inițială pe (−∞,∞)

$\{\begin{array}{cc}{u}_t=k{u}_{xx}& (x,t)\in ℝ\times (0,\mathrm{\infty })\\ u(x,0)=g(x)& \text{conditia initiala}\end{array}$

$u(x,t)=\frac{1}{\sqrt{4\pi kt}}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\exp (-\frac{(x-y{)}^2}{4\lambda t})g(y)dy$

Soluția fundamentală a ecuației unidimensionale a căldurii. Roșu: valoarea în timp a $\mathrm{\Phi }(x,t)$. Albastru: valoarea în timp a $\mathrm{\Phi }(x_0,t)$ pentru două puncte alese Format:Math și Format:Math. Se observă diferiții timpi de creștere/întârzieri și a amplitudinilor.

Comentariu. Această soluție este convoluția față de variabila Format:Mvar a soluției fundamentale

$\mathrm{\Phi }(x,t):=\frac{1}{\sqrt{4\pi \lambda t}}\exp (-\frac{x^2}{4\lambda t}),$

și funcția Format:Math Numărul funcției lui Green al soluției fundamentale este X00.

Prin urmare, conform proprietăților generale ale convoluției în raport cu diferențierea, Format:Math este o soluție a aceleiași ecuații a căldurii, pentru

$({\partial }_t-\lambda \underset{x}{\overset{2}{\partial }})(\mathrm{\Phi }*g)=\left[({\partial }_t-\lambda \underset{x}{\overset{2}{\partial }})\mathrm{\Phi }\right]*g=0.$

În plus,

$\mathrm{\Phi }(x,t)=\frac{1}{\sqrt{t}}\mathrm{\Phi }(\frac{x}{\sqrt{t}},1)$

$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\mathrm{\Phi }(x,t)dx=1,$

astfel încât, în general privind aproximarea cu identitatea, Format:Math când Format:Math în diverse sensuri, în funcție de Format:Mvar specifică. De exemplu, dacă Format:Mvar este considerată mărginitî și continuă pe Format:Math, atunci Format:Math converge uniform către Format:Mvar când Format:Math, ceea ce înseamnă că Format:Math este continuă pe Format:Math cu Format:Math

Problema valorii inițiale pe (0,∞) cu condiții la limită Dirichlet omogene

$\{\begin{array}{cc}{u}_t=k{u}_{xx}& (x,t)\in [0,\mathrm{\infty })\times (0,\mathrm{\infty })\\ u(x,0)=g(x)& \text{conditia initiala}\\ u(0,t)=0& \text{conditia la limita}\end{array}$

$u(x,t)=\frac{1}{\sqrt{4\pi \lambda t}}\underset{0}{\overset{\mathrm{\infty }}{\int }}[\exp (-\frac{(x-y{)}^2}{4\lambda t})-\exp (-\frac{(x+y{)}^2}{4\lambda t})]g(y)dy$

Comentariu. Această soluție este obținută din formula anterioară așa cum este aplicată la datele Format:Math extinse în mod corespunzător la Format:Math, astfel încât să fie o Format:Ill-wd, adică Format:Math pentru orice Format:Mvar. Corespunzător, soluția problemei valorii inițiale pe (−∞,∞) este o funcție impară în raport cu variabila Format:Mvar pentru orice valoare lui Format:Mvar și satisface condițiile la limită Dirichlet omogene Format:Math Numărul funcției lui Green al acestei soluții este X10.

Problema valorii inițiale pe (0,∞) cu condiții la limită Neumann omogene

$\{\begin{array}{cc}{u}_t=k{u}_{xx}& (x,t)\in [0,\mathrm{\infty })\times (0,\mathrm{\infty })\\ u(x,0)=g(x)& \text{conditia initiala}\\ u_x(0,t)=0& \text{conditia la limita}\end{array}$

$u(x,t)=\frac{1}{\sqrt{4\pi \lambda t}}\underset{0}{\overset{\mathrm{\infty }}{\int }}[\exp (-\frac{(x-y{)}^2}{4\lambda t})+\exp (-\frac{(x+y{)}^2}{4\lambda t})]g(y)dy$

Comentariu. Această soluție este obținută din prima formulă așa cum este aplicată la datele Format:Math extinse în mod corespunzător la Format:Math, astfel încât să fie o Format:Ill-wd, adică Format:Math pentru orice Format:Mvar. Corespunzător, soluția problemei valorii inițiale pe (−∞,∞) este o funcție pară în raport cu variabila Format:Mvar pentru orice valoare lui Format:Math și, fiind netedă, satisface condițiile la limită Neumann omogene Format:Math Numărul funcției lui Green al acestei soluții este X20.

Problema pe (0,∞) cu condiții inițiale omogene și condiții la limită Dirichlet neomogene

$\{\begin{array}{cc}{u}_t=k{u}_{xx}& (x,t)\in [0,\mathrm{\infty })\times (0,\mathrm{\infty })\\ u(x,0)=0& \text{conditia initiala}\\ u(0,t)=h(t)& \text{conditia la limita }\end{array}$

$u(x,t)=\underset{0}{\overset{t}{\int }}\frac{x}{\sqrt{4\pi \lambda (t-s{)}^3}}\exp (-\frac{x^2}{4\lambda (t-s)})h(s)ds,\mathrm{\forall }x>0$

Comentariu. Această soluție este convoluția față de Format:Mvar a lui: $\psi (x,t):=-2\lambda {\partial }_x\mathrm{\Phi }(x,t)=\frac{x}{\sqrt{4\pi \lambda t^3}}\exp (-\frac{x^2}{4\lambda t})$ și funcția Format:Math Deoarece Format:Math este soluția fundamentală a

${\partial }_t-\lambda \underset{x}{\overset{2}{\partial }},$

funcția Format:Math este de asemenea o soluție a aceleiași ecuații a căldurii, la fel și Format:Math datorită proprietăților generale ale convoluției în raport cu diferențierea. În plus,

$\psi (x,t)=\frac{1}{x^2}\psi (1,\frac{t}{x^2})$

$\underset{0}{\overset{\mathrm{\infty }}{\int }}\psi (x,t)dt=1,$

ca urmare, în general privind aproximarea cu identitatea, Format:Math când Format:Math în diferite sensuri, în funcție de Format:Mvar specifică. De exemplu, dacă Format:Mvar este considerată continuă pe Format:Math cu suport în [0, ∞), atunci Format:Math converge uniform pe compacta la Format:Mvar când Format:Math ceea ce înseamnă că Format:Math este continuă pe Format:Math cu Format:Math

Ecuația căldurii neomogenă

O soluție numerică a ecuației neomogene a căldurii. Ecuația a fost rezolvată cu condițiile inițiale și la limită 0 și un termen sursă reprezentând un arzător.

Problemă pe (-∞,∞) condiții inițiale omogene

Comentariu. Această soluție este convoluția în Format:Math adică față de ambele variabile Format:Mvar și Format:Mvar ale soluției fundamentale

$\mathrm{\Phi }(x,t):=\frac{1}{\sqrt{4\pi \lambda t}}\exp (-\frac{x^2}{4\lambda t})$

și funcția Format:Math ambele înțelese așa cum sunt definite pe tot Format:Math și 0 în rest pentru Format:Math Se verifică că

$({\partial }_t-\lambda \underset{x}{\overset{2}{\partial }})(\mathrm{\Phi }*f)=f,$

care exprimat în limbajul distribuțiilor devine

$({\partial }_t-\lambda \underset{x}{\overset{2}{\partial }})\mathrm{\Phi }=\delta ,$

unde distribuția Format:Mvar este funcția lui Dirac, adică valoarea în 0.

Problemă pe (0,∞) cu condiții la limită Dirichlet omogene și condiții inițiale

$\{\begin{array}{cc}{u}_t=k{u}_{xx}+f(x,t)& (x,t)\in [0,\mathrm{\infty })\times (0,\mathrm{\infty })\\ u(x,0)=0& \text{conditia initiala}\\ u(0,t)=0& \text{conditia la limita}\end{array}$

$u(x,t)=\underset{0}{\overset{t}{\int }}\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{1}{\sqrt{4\pi \lambda (t-s)}}[\exp (-\frac{(x-y{)}^2}{4\lambda (t-s)})-\exp (-\frac{(x+y{)}^2}{4\lambda (t-s)})]f(y,s)dyds$

Comentariu. Această soluție este obținută din formula anterioară, așa cum este aplicată datelor Format:Math extinse corespunzător pe Format:Math astfel încât să fie o funcție impară a variabilei Format:Mvar, adică Format:Math pentru toate Format:Mvar și Format:Mvar. Corespunzător, soluția problemei neomogene de pe (−∞,∞) este o funcție impară față de variabila Format:Mvar pentru toate valorile lui Format:Mvar și satisface condiția la limită Dirichlet omogenă Format:Math

Problemă pe (0,∞) cu condiții la limită Neumann omogene și condiții inițiale

$\{\begin{array}{cc}{u}_t=k{u}_{xx}+f(x,t)& (x,t)\in [0,\mathrm{\infty })\times (0,\mathrm{\infty })\\ u(x,0)=0& \text{conditia initiala}\\ u_x(0,t)=0& \text{conditia la limita}\end{array}$

$u(x,t)=\underset{0}{\overset{t}{\int }}\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{1}{\sqrt{4\pi \lambda (t-s)}}[\exp (-\frac{(x-y{)}^2}{4\lambda (t-s)})+\exp (-\frac{(x+y{)}^2}{4\lambda (t-s)})]f(y,s)dyds$

Comentariu. Această soluție este obținută din prima formulă, așa cum este aplicată datelor Format:Math extinse corespunzător pe Format:Math astfel încât să fie o funcție pară a variabilei Format:Mvar, adică Format:Math pentru toate Format:Mvar și Format:Mvar. Corespunzător, soluția problemei neomogene de pe (−∞,∞) este o funcție pară față de variabila Format:Mvar pentru toate valorile lui Format:Mvar și, fiind o funcție netedă, satisface condiția la limită Neumann omogenă Format:Math

Aplicații

Ca prototip al ecuațiior cu derivate parțiale parabolice, ecuația căldurii este printre cele mai studiate subiecte în matematica pură, iar analiza sa este considerată fundamentală pentru domeniul mai larg al ecuațiilor cu derivate parțiale. Ecuația căldurii poate fi luată în considerare și pe Format:Ill-wd, conducând la multe aplicații geometrice. În urma lucrărilor lui Subbaramiah Minakshisundaram și Åke Pleijel, ecuația căldurii este strâns legată de Format:Ill-wd. O variantă neliniară a ecuației căldurii a fost introdusă în geometria diferențială de către James Eells și Joseph H. Sampson în 1964, inspirând introducerea Format:Ill-wd de către Richard S. Hamilton în 1982 și culminând cu demonstrarea conjecturii lui Poincaré de Grigori Perelman în 2003. Anumite soluții ale ecuației căldurii cunoscute sub numele de nuclee ale căldurii oferă informații subtile despre regiunea în care sunt definite, așa cum este exemplificat prin aplicarea lor la Format:Ill-wd.

Ecuația căldurii, împreună cu variantele acesteia, este de asemenea importantă în multe domenii ale științei și matematicii aplicate. În teoria probabilităților, ecuația căldurii este conectată cu studiul Format:Ill-wd și a mișcării browniene prin Format:Ill-wd. Format:Ill-wd din matematica finanțelor este o variantă mică a ecuației căldurii, iar ecuația lui Schrödinger din mecanica cuantică poate fi privită ca o ecuație a căldurii în Format:Ill-wd. În Format:Ill-wd ecuația căldurii este uneori folosită pentru a rezolva pixelarea și pentru a Format:Ill-wd. În urma introducerii de către Robert D. Richtmyer și John von Neumann a metodelor viscozității artificiale, soluțiile ecuațiilor căldurii au fost utile în formularea matematică a Format:Ill-wd. De asemenea, începând din anii 1950 soluțiile ecuației căldurii au primit multă atenție în literatura de specialitate a analizei numerice prin lucrările lui Jim Douglas, D.W. Peaceman și Henry Rachford Jr.

Note

Bibliografie

• Format:En icon Format:Citation
• Format:En icon Format:Citation
• Format:En icon Format:Citation
• Format:En icon Format:Citation
• Format:En icon Format:Citation
• Format:En icon Format:Citation

Lectură suplimentară

• Format:En icon Format:Citation
• Format:En icon Format:Citation
• Format:En icon Format:Citation
• Format:En icon Format:Citation
• Format:En icon Format:Citation
• Format:En icon Format:Citation
• Format:En icon Format:Citation

Legături externe

• Format:Commons category-inline
• Format:En icon Derivation of the heat equation

• Format:En icon Linear heat equations: Particular solutions and boundary value problems - from EqWorld
• Format:En icon Format:Cite webFormat:Cbignore