Cub trunchiat

Dual:Octaedru triakis

În geometrie cubul trunchiat este un poliedru arhimedic. Are 6 fețe octogonale regulate, 8 fețe triunghiulare echilaterale, 24 de vârfuri și 36 de laturi. Poate fi construit prin trunchierea tuturor celor 8 vârfuri ale unui cub la o treime din lungimea laturii inițiale.

Dacă cubul trunchiat are lungimea muchiei 1, dualul său, octaedrul triakis are laturi de două feluri, cu lungimile 2 și 2 + Format:Sqrt.

Are indicele de poliedru uniform U₀₉, indicele Coxeter C₂₁ și indicele Wenninger W₈.

Arie și volum

Aria A și volumul V ale unui cub trunchiat cu lungimea muchiei a sunt:

$\begin{array}{cccc}A& =2(6+6\sqrt{2}+\sqrt{3})a^2& & \approx 32,4346644a^2\\ V& =\frac{21+14\sqrt{2}}{3}{a}^3& & \approx 13,5996633a^3.\end{array}$

Proiecții ortogonale

Cubul trunchiat are cinci proiecții ortogonale, centrate pe un vârf, cu două tipuri de laturi și două tipuri de fețe: triunghiuri și octogoane. Ultimele două corespund cu planele Coxeter B₂ și A₂.

Proiecții ortogonale

Centrată pe	Vârf	Latura 3-8	Latura 8-8	Fața octogon	Fața triunghi
Corp
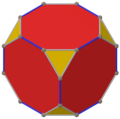
Cadru de sârmă
Dual
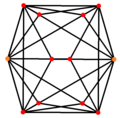
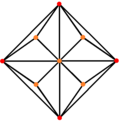
Simetrie proiectivă	[2]	[2]	[2]	[4]	[6]

Pavare sferică

Cubul trunchiat poate fi reprezentat și ca o pavare sferică și proiectat pe plan printr-o proiecție stereografică. Această proiecție este conformă, păstrând unghiurile, dar nu ariile sau lungimile. Liniile drepte pe sferă sunt proiectate în plan ca arce de cerc.

	centrată pe octogon	centrată pe triunghi
Proiecție ortogonală	Proiecții stereografice

Coordonate carteziene

Un cub trunchiat cu fețele sale octogonale piritoedrice divizat prin vârfuri din centrul fețelor în triunghiuri și pentagoane, creând topologic un icosidodecaedru

Coordonatele carteziene ale vârfurilor unui cub trunchiat centrat în origine cu lungimea laturii 2ξ sunt toate permutările lui

(±ξ, ±1, ±1),

unde ξ = Format:Sqrt − 1.

În afară de valoarea de mai sus, parametrul ξ poate lua valori între ±1. Valoarea 1 produce un cub, 0 produce un cuboctaedru, iar valorile negative produc fețe octagramice care se autointersectează.

Dacă porțiunile autointersectate ale octagramelor sunt îndepărtate, lăsând pătratele și trunchiind triunghiurile în hexagoane, se produc octaedre trunchiate, iar secvența se termină cu pătratele centrale reduse la un punct și creând un octaedru.

Divizare

Format:Imagine dublă Cubul trunchiat poate fi divizat într-un cub central, cu șase cupole pătrate în jurul fiecărei fețe a cubului și 8 tetraedre regulate în colțuri. Această divizare poate fi observată și în interiorul fagurelui cubic runcic, cu celule cubice, tetraedrice și rombicuboctaedrice.

Această divizare poate fi folosită pentru a crea un toroid Stewart cu toate fețele regulate prin îndepărtarea a două cupole pătrate și a cubului central. Acest cub excavat are 16 triunghiuri, 12 pătrate și 4 octogoane.

Dispunerea vârfurilor

Are aceeași dispunere a vârfurilor cu trei poliedre uniforme neconvexe:

Cub trunchiat

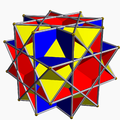Marele rombicuboctaedru neconvex

Marele cubicuboctaedru

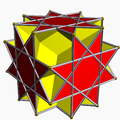Marele rombicuboctaedru

Poliedre înrudite

Cubul trunchiat este legat de alte poliedre și pavări prin simetrie.

Cubul trunchiat face parte dintr-o familie de poliedre uniforme înrudite cu cubul și octaedrul regulat. Format:Trunchieri octaedrice

Variante de simetrii

Acest poliedru este înrudit topologic ca parte a secvenței de poliedre trunchiate uniforme cu configurațiile vârfului (3.2n.2n) și [n,3] cu simetriile din grupul Coxeter și o serie de pavări n.8.8. Format:Tabel figuri1 trunchiate Format:Tabel figuri4 trunchiate

Trunchieri alternate

Format:Imagine multiplă Trunchierea alternată a vârfurilor cubului dă Format:Ill-wd, adică trunchierea laturilor tetraedrului.

Trapezoedrul triunghiular trunchiat este un alt poliedru care poate fi format prin trunchierea laturii cubului.

Politopuri înrudite

Cubul trunchiat este cel de-al doilea în secvența hipercuburilor trunchiate: Format:Hipercuburi trunchiate

Bibliografie

• Format:En icon Robert Williams (1979), The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications Inc., Format:ISBN. (Section 3-9)
• Format:En icon Cromwell, P. Polyhedra, CUP hbk (1997), pbk. (1999). Ch.2 p. 79-86 Archimedean solids

Vezi și

• Lista poliedrelor uniforme

Legături externe

• Format:En icon Format:Mathworld
• Format:En icon Format:Mathworld
• Format:En icon Format:Mathworld
• Format:En icon Editable printable net of a truncated cube with interactive 3D view
• Format:En icon The Uniform Polyhedra
• Format:En icon Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra

• Model VRML Format:Webarchive
• Conway Notation for Polyhedra Cheie: "tC"

• Format:En icon Format:KlitzingPolytopes Cheie: tic