Marele cubicuboctaedru
În geometrie marele cubicuboctaedru este un poliedru stelat uniform, cu indicele U14. Are 20 de fețe (8 triunghiuri, 6 pătrate și 6 octagrame), 48 de laturi și 24 de vârfuri.[1] Fețele pătrate și fețele octagramice sunt paralele cu cele ale unui cub, în timp ce fețele triunghiulare sunt paralele cu cele ale unui octaedru, de unde și numele de cubicuboctaedru. Prefixul mare servește să-l deosebească de micul cubicuboctaedru, care are și el fețele în direcțiile menționate mai sus.[2] Având 20 de fețe este un icosaedru neconvex. Un poliedru neconvex are fețe care se intersectează care nu reprezintă laturi sau fețe noi. Doar cele marcate cu sfere aurii sunt vârfuri, iar cele cu linii argintii sunt laturi.
Este reprezentat prin diagrama Coxeter–Dynkin Format:CDD. Figura vârfului este un patrulater autointersectat. Un poliedru neconvex are fețe care se intersectează care nu reprezintă muchii sau fețe noi. Doar cele marcate cu sfere aurii sunt vârfuri, iar cele cu linii argintii sunt laturi.
Are simbolul Wythoff 3 4 | 4/3.[1]
Mărimi asociate
Coordonate carteziene
Având același aranjament al vârfurilor cu cubul trunchiat, coordonatele carteziene ale vârfurilor, centrat în origine, cu lungimea laturii de 2, sunt toate permutările ale
Raza sferei circumscrise
Pentru lungimea laturii Format:Mvar raza sferei circumscrise este:[3]
Volum
Următoarea formulă pentru volum Format:Mvar este stabilită pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) Format:Mvar:
Proiecții ortogonale
Poliedre înrudite
Are în comun aranjamentul vârfurilor cu cubul trunchiat și cu alte două poliedre neconvexe. În plus, are în comun aranjamentul laturilor cu marele rombicuboctaedru neconvex (având în comun fețele triunghiulare și 6 fețe pătrate) și cu marele rombihexaedru (având fețele octagramice în comun).
 Cub trunchiat |
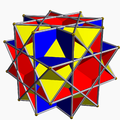 Marele rombicuboctaedru neconvex |
 Marele cubicuboctaedru |
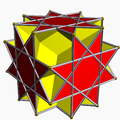 Marele rombihexaedru |

Poliedru dual
Dualul său este marele icositetraedru hexacronic.[3][4]
