Bitrunchiere

În geometrie o bitrunchiere este o operație pe politopuri regulate. Reprezintă o trunchiere dincolo de rectificare. Laturile inițiale se pierd complet, iar fețele inițiale rămân sub forma de copii mai mici ale lor.
Politopurile regulate bitrunchiate pot fi reprezentate printr-o notație cu simboluri Schläfli extinse t1,2{p,q,...} sau 2t{p,q,...}.
La poliedrele și pavările regulate
La poliedrele regulate (adică 3-politopuri regulate), o formă bitrunchiată este poliedrul dual trunchiat. De exemplu, un cub bitrunchiat este un octaedru trunchiat.
La 4-politopurile regulate și la faguri
La un 4-politop regulat, o formă bitrunchiată este un operator dual simetric. Un 4-politop bitrunchiat este același cu dualul bitrunchiat și va avea o simetrie dublă dacă 4-politopul inițial este autodual.
Un politop regulat (sau fagure) {p, q, r} va avea celulele {p, q} bitrunchiate la celule {q, p} trunchiate, iar vârfurile sunt înlocuite cu celule trunchiate {q, r}.
4-politopuri/faguri autoduali {p, q, p}
Un rezultat interesant al acestei operații este că 4-politopurile {p, q, p} (și fagurii) autoduali rămân tranzitivi pe celule după bitrunchiere. Există 5 astfel de forme care corespund celor cinci poliedre regulate trunchiate: t{q,p}. Doi sunt faguri pe 3-sferă, unul este un fagure în spațiul euclidian tridimensional și doi sunt faguri în spațiul hiperbolic tridimensional.
| Spațiu | 4-politop sau fagure | Simbol Schläfli Diagramă Coxeter–Dynkin |
Tip celulă | Imagine celulă |
Figura vârfului |
|---|---|---|---|---|---|
| 5-celule bitrunchiat (10-celule) (4-politop uniform) |
t1,2{3,3,3} Format:CDD |
Tetraedru trunchiat | 
|

| |
| 24-celule bitrunchiat (48-celule) (4-politop uniform) |
t1,2{3,4,3} Format:CDD |
Cub trunchiat | 
|

| |
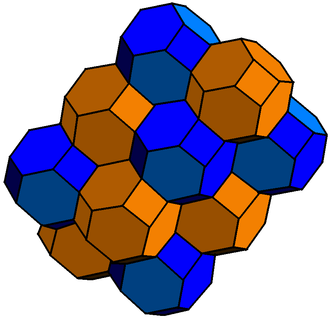
| Fagure cubic bitrunchiat (Fagure convex euclidian uniform) |
t1,2{4,3,4} Format:CDD |
Octaedru trunchiat | 
|

| |
| Fagure icosaedric bitrunchiat (Fagure uniform în spațiul hiperbolic) |
t1,2{3,5,3} Format:CDD |
Dodecaedru trunchiat | 
|

| |
| Fagure dodecaedric de ordinul 5 bitrunchiat (Fagure uniform în spațiul hiperbolic) |
t1,2{5,3,5} Format:CDD |
Icosaedru trunchiat | 
|

|
Bibliografie
- Format:En icon Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, Format:ISBN (pp. 145–154 Chapter 8: Truncation)
- Format:En icon Norman Johnson, Uniform Polytopes, Manuscript (1991)
- Format:En icon Norman Johnson, The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Format:En icon John Horton Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, Format:ISBN (Chapter 26)