Tetraedru trunchiat

În geometrie tetraedrul trunchiat este un poliedru arhimedic. Are 4 fețe hexagoane regulate, 4 fețe triunghiuri echilaterale, 12 vârfuri și 18 laturi (de două tipuri). Poate fi construit prin trunchierea tuturor celor 4 vârfuri ale unui tetraedru regulat la o treime din lungimea laturii inițiale.

O trunchiere mai intensă, care elimină din fiecare vârf câte un tetraedru cu latura jumătate din lungimea laturii inițiale, se numește rectificare și transformă tetraedrul într-un octaedru.

Tetraedrul trunchiat poate fi considerat un cub cantic, cu diagrama Coxeter, Format:CDD, aând jumătate din vârfurile unui cub cantelat (rombicuboctaedru), Format:CDD. Există două poziții duale ale acestei construcții, iar combinarea lor creează compusul uniform de două tetraedre trunchiate.

Are indicele de poliedru uniform U₀₂, indicele Coxeter C₁₆ și indicele Wenninger W₆.

Mărimi asociate

Coordonate carteziene

Coordonatele carteziene ale celor 12 vârfuri ale tetraedrului trunchiat centrat în origine, cu lungimea laturii Format:Sqrt sunt permutările lui (±1,±1,±3) cu un număr par de semne minus:

• (+3,+1,+1), (+1,+3,+1), (+1,+1,+3)
• (−3,−1,+1), (−1,−3,+1), (−1,−1,+3)
• (−3,+1,−1), (−1,+3,−1), (−1,+1,−3)
• (+3,−1,−1), (+1,−3,−1), (+1,−1,−3)

Arie și volum

Aria A și volumul V ale unui tetraedru trunchiat cu lungimea laturii a sunt:

$A=7\sqrt{3}{a}^2\approx 12,1243556a^2,$

$V=\frac{23}{12}\sqrt{2}{a}^3\approx 2,710576a^3.$

Proiecții

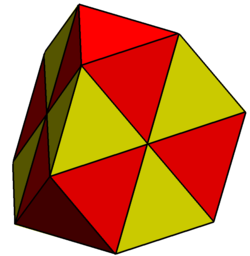
Proiecție ortogonală în coordonate carteziene în cubul de încadrare (±3,±3,±3).	Fețele hexagonale ale tetraedrelor trunchiate pot fi împărțite în 6 triunghiuri echilaterale coplanare. Cele 4 noi vârfuri au coordonatele carteziene: (−1,−1,−1), (−1,+1,+1), (+1,−1,+1), (+1,+1,−1). Astfel poate fi descompus în 4 octaedre (roșii) și 6 tetraedre (galbene).	Setul de permutări ale vârfurilor (±1,±1,±3) cu un număr impar de semne minus formează un tetraedru trunchiat complementar, care combinat cu cel inițial formează un compus uniform.

Proiecții ortogonale

Centrat pe	Normala laturii	Normala feței	Latură	Față
Proiecție
Cadru de sârmă
Dual
Simetrie proiectivă	[1]	[1]	[4]	[3]

Pavare sferică

Tetraedrul trunchiat poate fi reprezentat și ca o pavare sferică și proiectat în plan printr-o proiecție stereografică. Această proiecție este conformă, păstrând unghiurile, dar nu și ariile sau lungimile. Liniile „drepte” pe sferă sunt proiectate în plan ca arce de cerc.

	centrat pe triunghiuri	centrat pe hexagoane
Proiecție ortogonală	Proiecții stereografice

Poliedre înrudite

Dual: Tetraedru triakis

Format:Trunchieri tetraedrice Este, de asemenea, o parte dintr-un set de poliedre cantice și pavări cu configurația vârfului 3.6.n.6. În această construcție Wythoff, laturile dintre hexagoane reprezintă digoane degenerate.

Variante de simetrie

Acest poliedru este înrudit topologic de familia de poliedre trunchiate uniforme cu simetriile din grupul Coxeter ale configurațiilor vârfurilor (3.2n.2n) și [n,3].

Bibliografie

• Format:En icon Robert Williams (1979), The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications Inc., Format:ISBN. (Section 3-9)
• Format:En icon Format:Citation

Vezi și

• Lista poliedrelor uniforme

Legături externe

• Format:Commonscat-inline
• Format:En icon Format:Mathworld
• Format:En icon Format:Mathworld
• Format:En icon Editable printable net of a truncated tetrahedron with interactive 3D view
• Format:En icon The Uniform Polyhedra
• Format:En icon Virtual Reality Polyhedra The Encyclopedia of Polyhedra

• Format:En icon Format:KlitzingPolytopes Cheie: tut