Vector izotrop

Un con nul, unde $q(x,y,z)=x^2+y^2-z^2$

În matematică, fiind dat un spațiu vectorial Format:Mvar cu o formă pătratică asociată Format:Mvar un vector izotrop — numit și vector nul al formei pătratice — este un vector Format:Math astfel încât Format:Math.

Dacă o forma pătratică Format:Mvar admite un vector izotrop, atunci se numește formă pătratică izotropă. O formă pătratică care nu admite niciun vector izotrop se numește formă pătratică definită. Un spațiu pătratic Format:Math care are un vector izotrop se numește Format:Ill-wd.

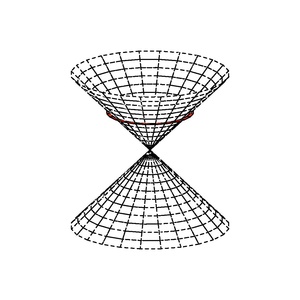
Un spațiu vectorial pseudoeuclidian poate fi descompus (neunic) în subspații ortogonale Format:Mvar și Format:Mvar astfel încât Format:Mvar este definită-pozitivă pe Format:Mvar și definită-negativă pe Format:Mvar. Conul izotrop (sau conul nul), al lui Format:Mvar constă din reuniunea sferelor echilibrate:

$\bigcup _{r\ge 0}\{x=a+b:q(a)=-q(b)=r,a\in A,b\in B\}.$

Conul izotrop este, de asemenea, reuniunea dreptelor izotrope care se intersectează în origine.

Exemple

Vectorii de tip „lumină” dintr-un spațiu Minkowski sunt vectori izotropi.

Cei patru Format:Ill-wd Format:Ill-wd Format:Math, Format:Math, Format:Math și Format:Math sunt vectori izotropi, iar Format:Math} pot servi ca bază pentru subspațiul folosit pentru a reprezenta spațiu-timpul. Vectorii izotropi sunt de asemenea folosiți în abordarea Format:Ill-wd al varietăților spațiu-timp.

În Format:Ill-wd al unei Format:Ill-wd există vectori izotropi.

Bibliografie

• Format:En icon Format:Cite book
• Format:En icon Format:Cite book
• Format:En icon Format:Cite book