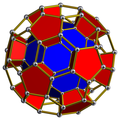
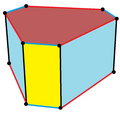
Prismă hexagonală

În geometrie prisma hexagonală este o prismă cu baza hexagonală. Are 8 fețe, 18 laturi și 12 vârfuri.[1] Deoarece are 8 fețe, în principiu este un octaedru. Totuși, de obicei termenul de „octaedru” este folosit în primul rând pentru a se referi la octaedrul regulat, care are opt fețe triunghiulare. Din cauza ambiguității, termenul de „octaedru” este rareori folosit fără alte precizări.
Prisma hexagonală uniformă are indicele de poliedru uniform U76d.[2]
Unele dintre cele mai comune obiecte în formă de prismă hexagonală sunt creioanele înainte de a fi ascuțite.[3]
Ca poliedru semiregulat (sau uniform)
Dacă fețele sunt toate regulate, prisma hexagonală este un poliedru semiregulat, mai general, un poliedru uniform, fiind a patra într-un set infinit de prisme formate din fețe laterale pătrate și două baze poligoane regulate. Poate fi văzut ca un hosoedru hexagonal trunchiat, reprezentat de simbolul Schläfli t{2,6}. Alternativ, poate fi văzut ca produsul cartezian al unui hexagon regulat și al unui segment, și reprezentat prin produsul {6}×{}. Dualul unei prisme hexagonale este o bipiramidă hexagonală.
Grupul de simetrie al unei prisme hexagonale drepte este D6h de ordinul 24. Grupul de rotație este D6 de ordinul 12.
Formule
Ca la toate prismele, aria totală Format:Mvar este de două ori aria bazei (Format:Mvar) plus aria laterală, iar volumul Format:Mvar este produsul dintre aria bazei și înălțimea (distanța dintre planele celor două baze) Format:Mvar.
Pentru o prismă cu baza hexagonală regulată cu latura Format:Mvar, aria Format:Mvar are formula:[4][5]
Pentru Format:Mvar = 1 și Format:Mvar = 1 aria este ≈11,1961524.
Formula volumului Format:Mvar este:[4]
Pentru Format:Mvar = 1 și Format:Mvar = 1 volumul este ≈2,5980762.
Simetrie
Topologia unei prisme hexagonale uniforme poate avea variații geometrice cu simetrie inferioară:
| Nume | Prismă hexagonală regulată | Trunchi hexagonal | Prismă ditrigonală | Prismă triambică | Trapezoprismă ditrigonală |
|---|---|---|---|---|---|
| Simetrie | D6h, [2,6], (*622) | C6v, [6], (*66) | D3h, [2,3], (*322) | D3d, [2+,6], (2*3) | |
| Construcție | {6}×{}, Format:CDD | t{3}×{}, Format:CDD | Format:CDD | s2{2,6}, Format:CDD | |
| Imagine | 
|

|

|

| |
| Distorsionat | 
|
|
 
|

| |
Faguri și 4-politopuri
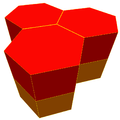
Prismele hexagonale apar ca celule în patru faguri convecși uniformi din spațiul tridimensional:
| Fagure prismatic hexagonal[1] Format:CDD |
Fagure prismatic triunghiular-hexagonal Format:CDD |
Fagure prismatic triunghiular-hexagonal snub Format:CDD |
Fagure prismatic rombitriunghiular-hexagonal Format:CDD |
|
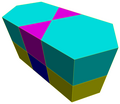
|

|

|
De asemenea, există ca celule ale unui număr de 4-politopuri uniforme, inclusiv:
Poliedre și pavări înrudite
Format:Trunchieri diedrice hexagonale Prisma hexagonală poate fi considerată ca făcând parte dintr-o secvență de modele uniforme cu figura vârfului (4.6.2p) și diagrama Coxeter–Dynkin Format:CDD. Pentru p < 6, membrii secvenței sunt poliedre omnitrunchiate (zonoedre), prezentate mai jos ca pavări sferice. Pentru p > 6, acestea sunt pavări ale planului hiperbolic, începând cu pavarea triheptagonală trunchiată. Format:Tabel omnitrunchiate
Note
- ↑ 1,0 1,1 Format:En icon Format:Citation.
- ↑ Format:En icon Format:Mathworld
- ↑ Format:En icon Format:Citation.
- ↑ 4,0 4,1 Format:De icon Regelmäßiges Prisma - Rechner, rechneronline.de, accesat 2022-06-28
- ↑ Format:En icon Format:Citation
Vezi și
Legături externe
- Format:En icon Uniform Honeycombs in 3-Space VRML models
- Format:En icon The Uniform Polyhedra
- Format:En icon Virtual Reality Polyhedra The Encyclopedia of Polyhedra Prisms and antiprisms
- Format:En icon Format:Mathworld
- Format:En icon Hexagonal Prism Interactive Model -- works in your web browser