Lunulă

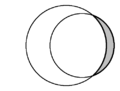
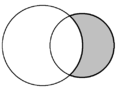
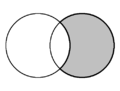
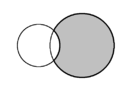
În geometria plană semiluna formată din două cercuri care se intersectează se numește lunulă. În diagrame sunt prezente câte două lunule, una fiind umbrită gri.

În geometria plană o lunulă este zona concav-convexă delimitată de două arce de cerc. Are o porțiune a frontierei pentru care segmentul dintre două puncte apropiate se află în întregime în afara zonei și o altă porțiune a frontierei pentru care segmentul dintre două puncte din apropiere se află în întregime în interiorul zonei. O zonă asemănătoare, dar convex-convexă, este denumită lentilă.

Formal, o lunulă este complementul relativ al unui disc cu care se intersectează, dar niciunul nu este inclus complet în celălalt. Alternativ, dacă $A$ și $B$ sunt discuri, atunci $A\setminus A\cap B$ este o lunulă.

Cvadratura lunulei

În secolul al V-lea î.Hr. Hipocrate din Chios a arătat că lunula lui Hipocrate și alte două lunule ar putea fi convertite într-un pătrat având aceeași arie folosind doar rigla și compasul. În 1766 matematicianul finlandez Daniel Wijnquist, citându-l pe Daniel Bernoulli, a enumerat toate cele cinci lunule care au cvadraturi, adăugându-le celor cunoscute de Hipocrate. În 1771, Leonard Euler a prezentat o abordare generală și o ecuație a problemei. În 1933 și 1947 a fost demonstrat de Nikolai Cebotariov și studentul său Anatoli Dorodnov că acestea cinci sunt singurele lunule care au cvadraturi.

Arie

Aria unei lunule formate din cercuri cu razele Format:Mvar și Format:Mvar (Format:Mvar) cu distanta Format:Mvar între centrele lor este

$A=2\mathrm{\Delta }+a^2{\sec }^{-1}\left(\frac{2ac}{b^2-a^2-c^2}\right)-b^2{\sec }^{-1}\left(\frac{2bc}{b^2+c^2-a^2}\right),$

unde ${\text{sec}}^{-1}$ este inversa secantei, iar

$\mathrm{\Delta }=\frac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}$

este aria triunghiului cu laturile Format:Mvar și Format:Mvar.

Legături externe

• Format:En icon The Five Squarable Lunes la MathPages