Piramidă alungită

În geometrie, piramida alungită este un poliedru convex, construit prin alungirea unei piramide n-gonale prin lipirea la baza piramidei a unei prisme n-gonale (bazele prismei și ale piramidei trebuie să fie congruente). Din punct de vedere topologic este autoduală.

Numărul piramidelor alungite este infinit, dar dintre ele trei sunt poliedre Johnson: piramida triunghiulară alungită (J₇), piramida pătrată alungită (J₈) și piramida pentagonală alungită (J₉). Piramide alungite cu n mai mari pot fi construite cu triunghiuri isoscele.

Formule

Pentru piramidele alungite se calculează separat aria piramidei Format:Mvar și aria laterală a prismei Format:Mvar. Aria piramidei alungite Format:Mvar va fi

$A=A_p+A_a.$

Pentru volum, se calculează separat volumul piramidei Format:Mvar și volumul prismei Format:Mvar. Volumul piramidei alungite Format:Mvar va fi

$V=V_p+V_a.$

Exemple

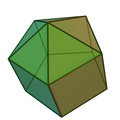
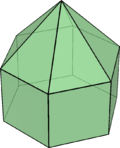
Nume	Piramidă triunghiulară alungită (J7)	Piramidă pătrată alungită (J8)	Piramidă pentagonală alungită (J9)	Piramidă hexagonală alungită (poliedru aproape Johnson)	Piramidă hexagonală alungită (cu triunghiuri isoscele)
Fețe	3+1 triunghiuri echilaterale, 3 pătrate	4 triunghiuri echilaterale, 4+1 pătrate	5 triunghiuri echilaterale, 5 pătrate, 1 pentagon	6 triunghiuri echilaterale, 6 pătrate, 1 hexagon	6 triunghiuri isoscele, 6 dreptunghiuri, 1 hexagon

Bibliografie

• Format:En icon Norman Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
• Format:En icon Format:Cite book The first proof that there are only 92 Johnson solids.

Vezi și

• Piramidă giroalungită
• Bipiramidă alungită
• Bipiramidă giroalungită