Pavare rombitrihexagonală

În geometrie, pavarea rombitrihexagonală este o pavare semiregulată a planului euclidian. În fiecare vârf se întâlnesc un triunghi, două pătrate și un hexagon. Are aimbolul Schläfli Format:Mvar{3,6}.
După terminologia lui Norman Johnson poate fi considerată o cantelare, iar în limbajul operațional al Aliciei Boole Stott o pavare hexagonală expandată.
Colorare uniformă
La o pavare rombitrihexagonală există o singură colorare uniformă. (Identificarea culorilor cu indici în jurul unui vârf (3.4.6.4): 1232.)
Cu colorarea laturilor există o formă cu jumătate de simetrie, notația orbifold (3*3). Hexagoanele pot fi considerate triunghiuri trunchiate, t{3} cu două tipuri de laturi. Are diagrama Coxeter Format:CDD, simbolul Schläfli Format:Mvar2{3,6}. Pătratul bicolor poate fi distorsionat în trapeze isoscele. La limită, când dreptunghiurile degenerează în laturi, rezultă o pavare triunghiulară, construită ca o pavare triunghiulară snub, Format:CDD.
| Simetrie | [6,3], (*632) | [6,3+], (3*3) | ||
|---|---|---|---|---|
| Nume | Rombitrihexagonală | Triunghiulară cantelată snub | Triunghiulară snub | |
| Imagine |  Colorare uniformă pe fețe |
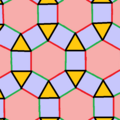 Colorare uniformă pe laturi |
 Geometrie neuniformă |
 La limită |
| simbol Schläfli |
rr{3,6} | s2{3,6} | s{3,6} | |
| Diagramă Coxeter |
Format:CDD | Format:CDD | Format:CDD | |
Exemple
 Din The Grammar of Ornament (1856) |
 Jocul Kensington |
 Pavare la Muzeul Arheologic din Sevilla |
 Templul Dianei de la Nîmes |
 Mozaic roman în Castelul di Guido |
Pavări înrudite

Există o pavare înrudită colorată 2-uniform, având hexagoanele divizate în câte 6 triunghiuri.[1][2] Pavarea rombitrihexagonală este înrudită și cu pavarea trihexagonală trunchiată prin înlocuirea unora dintre hexagoane și pătratele și triunghiurile din jur cu dodecagoane:
| 1-uniformă | Divizare | Divizări 2-uniforme | |
|---|---|---|---|
 3.4.6.4 |
 
|
 3.3.4.3.4 & 36 |
 la CH |
| Pavări duale | |||
 3.4.6.4 |
 
|
 4.6.12 |
 la 3 |
Împachetarea cercurilor

Pavarea rombitrihexagonală poate fi folosită la împachetarea cercurilor, plasând cercuri cu diametru egal în fiecare vârf. Fiecare cerc este în contact cu alte 4 cercuri din pavare (număr de contacte).[3].
Construcția Wythoff
Există opt pavări uniforme care pot fi bazate pe pavarea hexagonală regulată (sau pe duală, pavarea triunghiulară).
Desenând dalele colorate cu roșu pe fețele inițiale, galbene la vârfurile inițiale și albastre de-a lungul laturilor inițiale, există 8 forme, dintre care 7 sunt distincte topologic. (Pavarea triunghiulară trunchiată este identică din punct de vedere topologic cu pavarea hexagonală.)
Format:Pavări hexagonale regulate
Mutații de simetrie
Această pavare este legată din punct de vedere topologic ca parte a secvenței de poliedre cantelate figura vârfului (3.4.n.4) și continuă ca pavări ale planului hiperbolic. Aceste figuri tranzitive pe vârfuri au simetria în notația orbifold (*n32).
Note
- ↑ Format:En icon Format:Cite journal
- ↑ Format:En icon Format:Cite web
- ↑ Format:En icon Keith Critchlow, Order in Space: A design source book, p. 74-75, pattern B
Bibliografie
- Format:En icon Format:Cite book (Chapter 2.1: Regular and uniform tilings, p. 58-65)
- Format:En icon Williams, Robert, The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications, Inc., 1979, Format:ISBN, p/ 40
- Format:En icon John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, Format:Isbn [1] (Chapter 21, Naming Archimedean and Catalan polyhedra and tilings.
- Format:En icon Format:MathWorld
- Format:En icon Format:MathWorld
- Format:En icon Format:KlitzingPolytopes
- Format:En icon Keith Critchlow, Order in Space: A design source book, 1970, p. 69-61, Pattern N, Dual p. 77-76, pattern 2
- Format:En icon Dale Seymour, Jill Britton, Introduction to Tessellations, 1989, Format:Isbn, pp. 50–56, dual p. 116