Elice (matematică)

elicea „pe dreapta” (cos t, sin t, t) de la Format:Math până la Format:Math cu săgeți care arată direcția creșterii Format:Mvar

În matematică o elice este un tip de curbă în spațiu netedă, având tangentele la un unghi constant față de o axă fixă. Are o formă asemănătoare unui tirbușon. Elicele sunt importante în biologie, deoarece molecula de ADN are forma unei elice duble, iar multe proteine au substructuri elicoidale, cunoscute sub numele de elice alfa. Cuvântul elice provine din Format:Gr = întors, curbat. O elice „plină”, de exemplu o rampă elicoidală este un elicoid.

Proprietăți și tipuri

Pasul unei elice este înălțimea unei rotații complete a elicei, măsurată paralel cu axa ei.

O elice dublă constă din două elice (de obicei congruente) cu aceeași axă, care diferă printr-o translație de-a lungul axei.

O elice cilindrică (adică una cu rază constantă) are curbura și torsiunea constante.

O elice conică, cunoscută și ca spirală conică, poate fi definită drept o Format:Ill-wd pe o suprafață conică, cu distanța până la apex dată de o funcție exponențială a unghiului care indică direcția față de axă.

O curbă strâmbă se numește elice generalizată când tangentele sale fac un unghi constant cu o dreaptă din spațiu. O curbă strâmbă este o elice generalizată dacă și numai dacă raportul dintre curbură și torsiune este constant.

O curbă se numește elice înclinată dacă normala sa principală formează un unghi constant cu o dreaptă fixă din spațiu. Poate fi construită prin aplicarea unei transformări sistemului de coordonate în mișcare al unei elice generalizate.

Orientare

Comparație între două elice, demonstrând chiralitatea. Una este pe stânga, iar cealaltă pe dreapta. Pe fiecare rând comparația se face din alt punct de vedere.

Elicile pot fi pe dreapta și pe stânga. Privind de-a lungul axei elicei, dacă o mișcare de înșurubare în sensul acelor de ceasornic îndepărtează elicea de observator, atunci se numește elice „pe dreapta”, iar dacă se apropie de observator, atunci este o elice „pe stânga”. Chiralitatea este o proprietate a elicei, nu a perspectivei: o elice pe dreapta nu poate fi întoarsă pentru a arăta ca una pe stânga decât dacă este privită într-o oglindă, și invers.

Descriere matematică

Elicea formată de componentele sinusoidale x și y

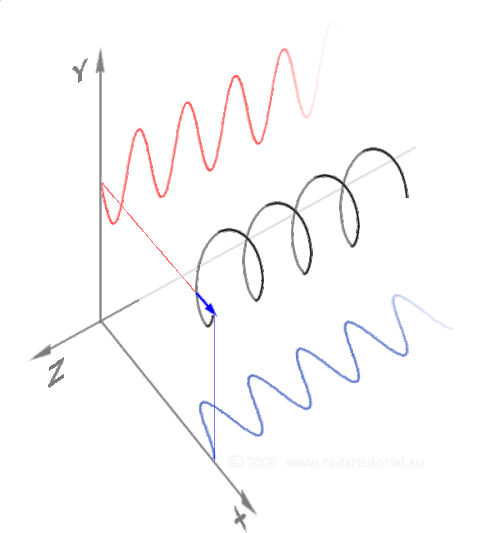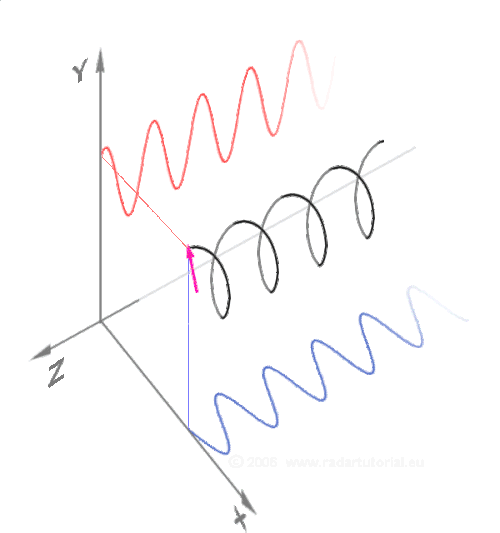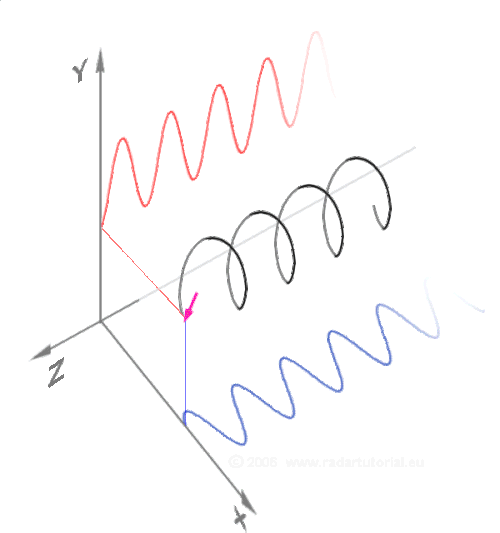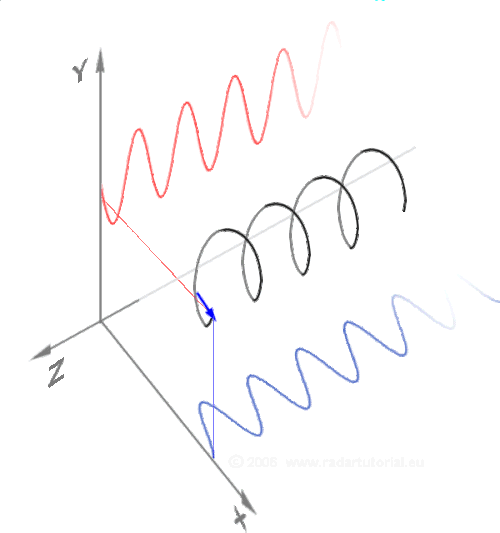
În matematică o spirală este o curbă diferențială tridimensională. Următoarea parametrizare în coordonate carteziene definește o anumită elice; poate cea mai simplă ecuație a unei elice este:

$x(t)=\cos (t),$

$y(t)=\sin (t),$

$z(t)=t.$

Când parametrul Format:Mvar crește, punctul (x(t),y(t),z(t)) descrie o elice pe dreapta cu pasul Format:Math (sau panta 1) și raza 1 în jurul axei Format:Mvar, într-un sistem de coordonate pe dreapta.

În coordonate cilindrice (r, θ, h), aceeași elice este parametrizată prin:

$r(t)=1,$

$\theta (t)=t,$

$h(t)=t.$

O elice cilindrică cu raza Format:Mvar și panta Format:Mvar (sau pasul Format:Math) este descrisă prin următoarea parametrizare:

$x(t)=a\cos (t),$

$y(t)=a\sin (t),$

$z(t)=bt.$

Un alt mod de a construi matematic o elice este de a reprezenta grafic funcția complexă Format:Mvar ca o funcție de numărul real Format:Mvar (vezi formula lui Euler). Valoarea lui Format:Mvar și părțile reale și imaginare ale valorii funcției dau acestui grafic trei dimensiuni reale.

Toate elicele drepte se pot obține in elicea definită mai sus prin operații de rotație translație și scalare. Elicea pe stânga echivalentă poate fi construită în mai multe moduri, cel mai simplu fiind de a schimba semnul uneia dintre componentele Format:Mvar, Format:Mvar sau Format:Mvar.

Lungimea arcului, curbura și torsiunea

Lungimea arcului a unei elice cilindrice cu raza Format:Mvar și panta Format:Mvar (sau pasul Format:Math) exprimată în coordonate dreptunghiulare ca

$t\mapsto (a\cos t,a\sin t,bt),t\in [0,T]$

este $T\cdot \sqrt{a^2+b^2}$, curbura este $\frac{|a|}{a^2+b^2},$ iar torsiunea este $\frac{b}{a^2+b^2}.$ O elice are curbura și torsiunea constantă, diferite de zero.

O elice este funcția cu valorile vectoriale

$𝐫=a\cos t𝐢+a\sin t𝐣+bt𝐤$

$𝐯=-a\sin t𝐢+a\cos t𝐣+b𝐤$

$𝐚=-a\cos t𝐢-a\sin t𝐣+0𝐤$

$|𝐯|=\sqrt{(-a\sin t{)}^2+(a\cos t{)}^2+b^2}=\sqrt{a^2+b^2}$

$|𝐚|=\sqrt{(-a\sin t{)}^2+(a\cos t{)}^2}=a$

$s(t)=\underset{0}{\overset{t}{\int }}\sqrt{a^2+b^2}d\tau =\sqrt{a^2+b^2}t$

Deci, o elice poate fi reparametrizată în funcție de $s$, care trebuie să fie unitatea de viteză:

$𝐫(s)=a\cos \frac{s}{\sqrt{a^2+b^2}}𝐢+a\sin \frac{s}{\sqrt{a^2+b^2}}𝐣+\frac{bs}{\sqrt{a^2+b^2}}𝐤$

Versorul tangent este

$\frac{d𝐫}{ds}=𝐓=\frac{-a}{\sqrt{a^2+b^2}}\sin \frac{s}{\sqrt{a^2+b^2}}𝐢+\frac{a}{\sqrt{a^2+b^2}}\cos \frac{s}{\sqrt{a^2+b^2}}𝐣+\frac{b}{\sqrt{a^2+b^2}}𝐤$

Vectorul normal este

$\frac{d𝐓}{ds}=\kappa 𝐍=\frac{-a}{a^2+b^2}\cos \frac{s}{\sqrt{a^2+b^2}}𝐢+\frac{-a}{a^2+b^2}\sin \frac{s}{\sqrt{a^2+b^2}}𝐣+0𝐤$

Curbura este

$\left|\frac{d𝐓}{ds}\right|=\kappa =\frac{|a|}{a^2+b^2}$.

Versorul normal este

$𝐍=-\cos \frac{s}{\sqrt{a^2+b^2}}𝐢-\sin \frac{s}{\sqrt{a^2+b^2}}𝐣+0𝐤$

Vectorul binormal este

$𝐁=𝐓\times 𝐍=\frac{1}{\sqrt{a^2+b^2}}[b\sin \frac{s}{\sqrt{a^2+b^2}}𝐢-b\cos \frac{s}{\sqrt{a^2+b^2}}𝐣+a𝐤]$

$\frac{d𝐁}{ds}=\frac{1}{a^2+b^2}[b\cos \frac{s}{\sqrt{a^2+b^2}}𝐢+b\sin \frac{s}{\sqrt{a^2+b^2}}𝐣+0𝐤]$

Torsiunea este

$\tau =\left|\frac{d𝐁}{ds}\right|=\frac{b}{a^2+b^2}$.

Exemple

În biologia moleculară un exemplu de elice dublă este cea a ADN.

Unele curbe găsite în natură constau din mai multe elice, pe stânga sau pe dreapta.

În tehnică exemple de elice sunt filetele șuruburilor, care pot fi pe dreapta sau pe stânga. Alt exemplu sunt arcurile elicoidale. În aviație „pasul elicei” este distanța în care o elice avansează la o rotație.

• 
  Dubla elice a ADN
• 
  O elice pe stânga a unei plante agățătoare
• 
  Traiectoria unei particule încărcate electric într-un câmp magnetic uniform
• 
  Un arc elicoidal

Vezi și

• Elice Boerdijk–Coxeter
• Solenoid