Dodecaedru disdiakis

Dual: Cuboctaedru trunchiat

În geometrie un dodecaedru disdiakis este un poliedru Catalan cu 48 de fețe. Fiecare poliedru Catalan este dualul unui poliedru arhimedic. Dualul tetraedrului disdiakis este cuboctaedrul trunchiat. Este tranzitiv pe fețe, însă fețele sale sunt poligoane neregulate. Seamănă cu un dodecaedru rombic. Înlocuirea fiecărei fețe a dodecaedrului rombic cu o piramidă plată creează un poliedru care arată aproape ca dodecaedrul disdiakis și este topologic echivalent cu acesta. Formal, dodecaedrul disdiakis este un Kleetop al dodecaedrului rombic. Desfășurata piramidei cubotaedrice are aceeași topologie.

Proiectat într-o sferă, laturile unui dodecaedru disdiakis definesc 9 cercuri mari. Buckminster Fuller a folosit aceste 9 cercuri mari, împreună cu alte 12 și alte 4 din alte două poliedre pentru a-și defini cele 25 de cercuri mari ale octaedrului sferic.

Simetrie

Are simetrie octaedrică O_h. Laturile sale definesc planele de reflexie ale simetriei. Poate fi văzut și ca triangulare a colțului și a mijlocului laturii cubului și octaedrului regulat, și a dodecaedrului rombic.

Dodecaedru disdiakis

Icositetraedru deltoidal

Dodecaedru rombic

Cub

Octaedru

Poliedru sferic
(animație)	Proiecții ortogonale după axele cu 2, 3 și 4 poziții

Laturile unui dodecaedru disdiakis sferic se află pe 9 cercuri mari. Trei dintre ele formează un octaedru sferic (gri în imaginile de mai jos). Restul de șase formează trei hosoedre pătrate (roșu, verde și albastru în imaginile de mai jos). Toate corespund planelor de oglindire — primul în simetrie diedrală [2,2], iar cel de-al doilea în simetrie tetraedrică [3,3].

Proiecții stereografice
	cu 2 poziții	cu 3 poziții	cu 4 poziții

Coordonate carteziene

Fie a = 1/(1 + 2Format:Sqrt), b = 1/(2 + 3Format:Sqrt) și c = 1/Format:Sqrt.
Atunci coordonatele carteziene pentru vârfurile unui dodecaedru disdiakis centrat în origine sunt:

• toate permutările lui (±a, 0, 0)
• toate permutările lui (±b, ±b, 0)
• (±c, ±c, ±c).

Aceste numere au la bază cuboctaedrul dublu trunchiat cu lungimea laturii de 2.

Dimensiuni

Dacă laturile sale mici au lungimea a, aria și volumul acesteia sunt

$\begin{array}{ccc}A& =\frac{6}{7}\sqrt{783+436\sqrt{2}}{a}^2& \approx 32,06673401053a^2\\ V& =\frac{1}{7}\sqrt{3(2194+1513\sqrt{2})}{a}^3& \approx 16,28891908292a^3\end{array}$

Fețele sunt triunghiuri scalene. Unghiurile lor sunt $\arccos (\frac{1}{6}-\frac{1}{12}\sqrt{2})\approx 87,20196376796^{\circ }$, $\arccos (\frac{3}{4}-\frac{1}{8}\sqrt{2})\approx 55,02469614890^{\circ }$ și $\arccos (\frac{1}{12}+\frac{1}{2}\sqrt{2})\approx 37,77334008313^{\circ }$.

Proiecții ortogonale

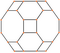
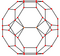
Cuboctaedrul trunchiat și dualul său, dodecaedrul disdiyakis pot fi reprezentate într-un număr de orientări proiective ortogonale simetrice. Între un poliedru și dualul său, vârfurile și fețele sunt interschimbate, iar laturile sunt perpendiculare.

Simetrie proiectivă	[4]	[3]	[2]	[2]	[2]	[2]	[2]+
Imagine
Imagine dual

Poliedre și pavări înrudite

Poliedrele similare cu dodecaedrul disdiakis sunt duale cu octaedrul și cubul „papion”, conținând perechi suplimentare de fețe triunghiulare.

Dodecaedrul disdiakis face parte dintr-o familie de duale ale poliedrelor uniforme legate de cub și octaedrul regulat. Format:Trunchieri octaedrice

Este un poliedru într-o secvență definită de configurația feței V4.6.2n. Acest grup este particular pentru că toate au un număr par de laturi la vârfuri și formează plane care divid poliedrele în două părți egale și continuă în planul hiperbolic pentru orice „n” ≥ 7.

Cu un număr par de fețe la fiecare vârf, aceste poliedre și pavări pot fi afișate colorate alternativ cu două culori, astfel încât toate fețele adiacente să aibă culori diferite.

Fiecare față a acestor figuri corespunde domeniul fundamental al unui grup de simetrie de ordinul 2,3,n oglindiri în fiecare vârf al feței triunghiulare. Format:Tabel figuri1 trunchiate

Bibliografie

• Format:En icon Format:Cite book (Section 3-9)
• Format:En icon John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss (2008), The Symmetries of Things, Format:ISBN [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 285, kisRhombic dodecahedron)

Legături externe

• Format:En icon Format:Mathworld
• Format:En icon Format:Mathworld
• Format:En icon Disdyakis Dodecahedron (Hexakis Octahedron) Interactive Polyhedron Model