Descompunerea unui vector

În teoria vectorilor, descompunerea unui vector din ${ℝ}^n$ reprezintă obținerea unui sistem echivalent de n vectori liniari independenți și situați pe direcții distincte.

Descompunerea unui vector după două direcții concurente

Descompunerea unui vector $\overrightarrow{V}$ după două direcții concurente d₁ și d₂ înseamnă determinarea sistemului de vectori concurenți ${\overrightarrow{V}}_1$ și ${\overrightarrow{V}}_2$ a căror rezultantă este vectorul $\overrightarrow{V}$ sau determinarea componentelor ${\overrightarrow{V}}_1$ și ${\overrightarrow{V}}_2$ ale acestuia pe cele două direcții d₁ și d₂.

Folosind regula paralelogramului, prin extremitatea vectorului $\overrightarrow{V}$ se construiesc paralele la direcțiile d₁ și d₂, punctele de intersecție cu aceste direcții definind extremitățile vectorilor ${\overrightarrow{V}}_1$ și ${\overrightarrow{V}}_2$.

Descompunerea unui vector după trei direcții concurente în spațiu

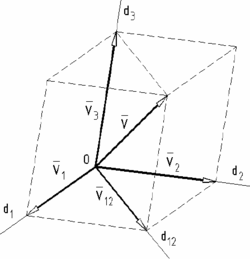
Se aplică regula paralelogramului în două etape. În prima etapă, se descompune vectorul $\overrightarrow{V}$ după una dintre cele trei direcții, spre exemplu d₃ și o direcție d_1,2, obținută ca intersecție dintre planul format de celelalte două direcții, d₁ și d₂ cu planul format de cea de-a treia direcție d₃ și vectorul $\overrightarrow{V}$, rezultând componentele ${\overrightarrow{V}}_3$ și ${\overrightarrow{V}}_{1,2}$.

În etapa a doua se descompune componenta ${\overrightarrow{V}}_{1,2}$ după direcțiile d₁ și d₂ rezultând componentele ${\overrightarrow{V}}_1$ și ${\overrightarrow{V}}_2$. Vectorul $\overrightarrow{V}$ reprezintă diagonala paralelipipedului având ca muchii componentele ${\overrightarrow{V}}_1,V_2$ și ${\overrightarrow{V}}_3$.