Compus prismatic de antiprisme

În geometrie un compus prismatic de antiprisme este o categorie a compușilor poliedrici uniformi. Fiecare membru al acestei familii infinite de compuși poliedrici uniformi este un aranjament simetric de antiprisme care au o axă comună de simetrie de rotație.

Familia infinită

Această familie infinită poate fi enumerată astfel:

Pentru fiecare număr întreg pozitiv n ≥ 1 și pentru fiecare număr rațional p/q > 3/2 (unde p și q sunt coprime), apare compusul de antiprisme n p/q-gonale, cu grupul de simetrie:

• D_npd dacă nq este impar
• D_nph dacă nq este par

unde p/q = 2, componentul este tetraedrul (sau antiprisma digonală). În acest caz, dacă n = 2 atunci compusul este stella octangula, cu simetrie mai mare (O_h).

Compuși de două antiprisme

Compușii de două n-antiprisme au vârfurile în comun cu o 2n-prismă și există ca două seturi de vârfuri alternante.

Coordonatele carteziene pentru vârfurile unei antiprisme cu baze n-gonale și fețele laterale triunghiuri isoscele sunt

$(\cos \frac{k\pi }{n},\sin \frac{k\pi }{n},(-1{)}^{k}h)$

$(\cos \frac{k\pi }{n},\sin \frac{k\pi }{n},(-1{)}^{k+1}h)$

cu k având valori de la 0 la 2n−1. Dacă triunghiurile sunt echilaterale,

$2h^2=\cos \frac{\pi }{n}-\cos \frac{2\pi }{n}.$

Compuși de 2 antiprisme

Format:CDD Format:CDD	Format:CDD Format:CDD	Format:CDD Format:CDD	Format:CDD Format:CDD	Format:CDD Format:CDD
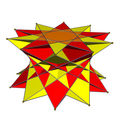
2 antiprisme digonale (tetraedre)	2 antiprisme triunghiulare (octaedre)	2 antiprisme pătrate	2 antiprisme hexagonale	2 antiprisme stelate pentagramice

Compuși de două trapezoedre (duali)

Dualii compușilor prismatici de antiprisme sunt compuși de trapezoedre:

Două cuburi (trapezoedre trigonale)

Compuși de trei antiprisme

Pentru compușii cu trei antiprisme diagonale, acestea sunt rotite cu 60 de grade, în timp ce trei antiprisme triunghiulare sunt rotite cu 40 de grade.

Trei tetraedre	Trei octaedre

Vezi și

• Lista compușilor poliedrici uniformi

Compuși prismatici

• Compus prismatic de prisme
• Compus prismatic de prisme cu libertate de rotație
• Compus prismatic de antiprisme cu libertate de rotație