Pavare pătrată trunchiată
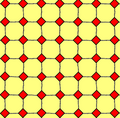
În geometrie o pavare pătrată trunchiată este o pavare semiregulată a planului euclidian cu câte un pătrat și două octogoane în fiecare vârf. Aceasta este singura pavare latură la latură cu poligoane regulate convexe care conține octogoane. Are simbolul Schläfli t{4,4}.
Alte denumiri folosite pentru acest model sunt pavare mediterană și pavare octogonală, care este adesea formată din pătrate mai mici și octogoane neregulate, la care laturile lungi și scurte alternează.
Colorare uniformă
Există două colorări uniforme distincte ale unei pavări pătrate trunchiate. (Identificarea culorilor în jurul unui vârf (4.8.8) se face cu indici: 122, 123.)
 2 culori: 122 Format:CDD |
 3 culori: 123 Format:CDD |
Împachetarea cercurilor

Pavarea pătrată trunchiată poate fi folosită la împachetarea cercurilor, plasând cercuri cu diametre egale în fiecare vârf. Fiecare cerc este în contact cu alte 3 cercuri din pachet (Format:Ill-wd).[1] Format:-
Variante
Format:Imagine multiplă O variantă a acestui model, adesea numită model mediteran, are pătrate mai mici, aliniate pe diagonală. Alte variante aplatizează pătratele sau octogoanele.
Pavarea pitagoreică alternează pătratele mari cu cele mici și poate fi considerată ca fiind identică din punct de vedere topologic cu pavarea pătrată trunchiată. Pătratele sunt rotite cu 45°, iar octogoanele sunt distorsionate în pătrate având vârfuri și la mijlocul laturilor.
Un model de țesătură are, și el, aceeași topologie, cu octogoane și dreptunghiuri aplatizate.
| p4m, (*442) | p4, (442) | p4g, (4*2) | pmm (*2222) | ||||
|---|---|---|---|---|---|---|---|

|
|

|

|

|

|

|

|
| p4m, (*442) | p4, (442) | cmm, (2*22) | pmm (*2222) | ||||

|

|

|

|

|

|

|

|
| Mediterană | Pitagoreică | Model flamand | Țesătură | Răsucit | Rectangular/rombic | ||
Poliedre și pavări înrudite

Pavarea pătrată trunchiată este legată topologic ca parte a secvenței de poliedre uniforme și pavări cu figura vârfului 4.2n.2n, extinzându-se în planul hiperbolic: Format:Tabel figuri3 trunchiate
Fagurele cubic bitrunchiat tridimensional proiectat în plan prezintă două copii ale unei pavări trunchiate. În plan, combinația lor poate fi reprezentată printr-o pavare compusă, sau poate fi văzută ca o pavare pătrată șanfrenată.
 Pavare pătrată trunchiată (prima variantă generată de fagure) Format:CDD |
 Pavare pătrată trunchiată (a doua variantă generată de fagure) Format:CDD |
 Compusul celor două pavări din stânga (Pavare pătrată șanfrenată) Format:CDD + Format:CDD |
Construcția Wythoff pentru pavarea pătrată
Desenând dalele colorate cu roșu în pavarea originală, cu galben cele din vârfurile originale trunchiate și cu albastru laturile originale, toate cele 8 forme sunt distincte. Totuși, tratând fețele în mod identic, există doar trei forme topologice unice: pavarea pătrată, pavarea pătrată trunchiată și pavarea pătrată snub. Format:Tabel pavare de ordinul 4-4
Pavări înrudite în alte simetrii
Format:Tabel omnitrunchiate4 Format:Tabel omnitrunchiate simetrice
Pavare pătrată tetrakis
Format:Imagine multiplă Pavarea pătrată tetrakis este duala pavării pătrate trunchiate. Poate fi construită din pavarea pătrată prin divizarea fiecărui pătrat în patru triunghiuri isoscele dreptunghice cu unghiurile drepte în punctul central al dalelor, formând un aranjament infinit de drepte. De asemenea, se poate forma prin subîmpărțirea fiecărui pătrat al unei grile în două triunghiuri printr-o diagonală, cu diagonalele alternând ca direcție, sau prin suprapunerea a două grile pătrate, una rotită cu 45° față de cealaltă și scalată cu un factor de Format:Sqrt.
Note
- ↑ Format:En icon Order in Space: A design source book, Keith Critchlow, p.74-75, circle pattern H
Bibliografie
- Format:En icon John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, Format:Isbn [1]
- Format:En icon Format:Cite book (Chapter 2.1: Regular and uniform tilings, p. 58-65)
- Format:En icon Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications, Inc. p. 40, Format:ISBN
- Format:En icon Dale Seymour, Jill Britton, Introduction to Tessellations, 1989, Format:Isbn, pp. 50–56