Micul icosicosidodecaedru

În geometrie micul icosicosidodecaedru este un poliedru stelat uniform, cu indicele U₃₁. Are 52 de fețe (20 de triunghiuri, 12 pentagrame și 12 decagrame), 120 de laturi și 60 de vârfuri. Având 52 de fețe, este un pentacontadiedru.

Este reprezentat prin diagramele Coxeter–Dynkin Format:CDD. Figura vârfului este un patrulater autointersectat. Un poliedru neconvex are fețe care se intersectează care nu reprezintă muchii sau fețe noi. Doar cele marcate cu sfere aurii sunt vârfuri, iar cele cu linii argintii sunt laturi.

Are simbolul Wythoff 5/2 3 | 3.

Mărimi asociate

Coordonate carteziene

Coordonatele carteziene ale vârfurilor unui mic dodecicosidodecaedru centrat în origine, cu lungimea laturii de 2, sunt toate permutările pare ale:

$(\pm 1,\pm 2\phi ,\pm (\phi -1))$

$(0,\pm (\phi +1),\pm (2\phi -1))$

$(\pm 1,\pm 2,\pm (\phi +1))$

unde $\phi =\frac{1+\sqrt{5}}{2}$ este secțiunea de aur.

Raza sferei circumscrise

Raza sferei circumscrise pentru lungimea laturii egală cu Format:Mvar este:

$R=\frac{1}{4}\sqrt{34+6\sqrt{5}}a\approx 1,721489a.$

Volum

Următoarea formulă pentru volum Format:Mvar este stabilită pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) Format:Mvar:

$V=(10+\frac{29}{3}\sqrt{5})a^3\approx 31,615324a^3$

Poliedre înrudite

Are în comun aranjamentul vârfurilor cu marele dodecaedru trunchiat stelat. În plus, are în comun aranjamentul laturilor cu micul icosicosidodecaedru ditrigonal (având fețele triunghiulare și pentagramice în comun) și cu micul dodecicosaedru (având fețele hexagonale în comun).

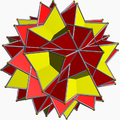Marele dodecaedru trunchiat stelat

Micul icosicosidodecaedru

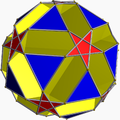Micul dodecicosidodecaedru ditrigonal

Micul dodecicosaedru

Dual: micul hexaconatedru icosacronic

Poliedru dual

Dualul său este micul hexaconatedru icosacronic.

Bibliografie

• Format:En icon Format:Cite journal
• Format:En icon Format:Cite book

Legături externe

• Format:En icon Uniform polyhedra and duals

• Format:En icon Format:KlitzingPolytopes Cheie: siid