Octagramă
Format:Infocaseta Poligon În geometrie o octagramă este un poligon stelat cu opt vârfuri cu simbolul Schläfli {8/3}.
Denumirea de octagramă vine de la prefixul numeric grecesc „octa-” și sufixul din Format:Gr, care înseamnă „linie”.[1]
Detalii
În general, o octagramă este orice octogon (poligon cu 8 laturi) care se autointersectează.
Octagrama regulată are simbolul Schläfli {8/3}, ceea ce înseamnă o stea cu 8 laturi, cu laturile conectate din trei în trei vârfuri.
Aria sa pentru lungimea laturii Format:Math este:[2]

Variante
Aceste varante au o simetrie diedrală inferioară, Dih4:
 Îngustă  Lată (rotită cu 45°) |
  Izotoxală |
 Vechiul drapel al Chile conținea această stea octogonală cu laturile invizibile (Guñelve). |
 Geometria poate fi ajustată astfel încât 3 laturi să se intersecteze într-un singur punct, cum ar fi în simbolul Auseklis |
 Roza vânturilor cu 8 direcții poate fi văzută ca o stea octogonală, cu 4 puncte principale și 4 puncte secundare. |
Simbolul Rub el Hizb este caracterul ۞ Unicode U+06DE. Format:Clear
Ca pătrat cvasitrunchiat
Trunchieri mai mari ale pătratului pot produce forme de poligoane stelate intermediare izogonale (tranzitive pe vârfuri) cu vârfuri egal distanțate și laturi de două lungimi. Un pătrat trunchiat este un octogon, t{4}={8}. Un pătrat cvasitrunchiat, inversat ca {4/3}, este o octagramă, t{4/3}={8/3}.[3]
Poliedrul stelat hexaedru trunchiat stelat, t'{4,3} = t{4/3,3} are fețe octagramice construite din cub. Din acest motiv poate fi considerat ca un analog tridimensional al octagramei.
| Regulat | Cvasiregulat | Izogonal | Cvasiregulat |
|---|---|---|---|
 {4} |
 t{4}={8} |

|
 t'{4}=t{4/3}={8/3} |
| Regulate | Uniform | Izogonal | Uniform |
 {4,3} |
 t{4,3} |

|
 t'{4,3}=t{4/3,3} |
O altă versiune tridimensională a octagramei este marele rombicuboctaedru neconvex (cvasirombicuboctaedrul), care poate fi considerat un cub cvasicantelat (cvasiexpandat), t0,2{4/3,3}.
Compuși poligonali stelați
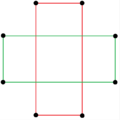
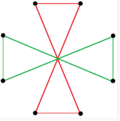
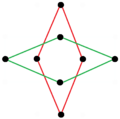
Există două stelări octagramice regulate (compuși) de forma {8/k}, prima construită din două pătrate {8/2}=2{4} și a doua din patru digoane degenerate, {8 /4}=4{2}. Există și alți compuși izogonali și izotaxali, inclusiv forme dreptunghiulare și rombice.
| Regulate | Izogonale | Izotoxal | ||
|---|---|---|---|---|
 a{8}={8/2}=2{4} |
 {8/4}=4{2} |
|
|
|
{8/2} sau 2{4}, ca diagramele Coxeter Format:CDD + Format:CDD, pot fi văzute drept echivalentul bidimensional al compusului de cub și octaedru tridimensional, Format:CDD + Format:CDD, al compusului de tesseract și 16-celule cvadridimensional, Format:CDD + Format:CDD, respectiv al compusului de 5-cub și 5-ortoplex pentadimensional, adică a compusului de n-cub și n-ortoplex în pozițiile lor duale.
Alte prezentări ale stelei octogonale
O „stea octogonală” poate fi văzută ca un hexadecagon concav, cu geometria din interior ștearsă. Poate fi divizat și prin drepte radiale.
| poligon stelat | Concav | Divizări prin centru | ||
|---|---|---|---|---|
 Compus 2{4} |
 |8/2| |

|

|

|
 Regulat {8/3} |
 |8/3| |

|

|

|
 Izogonal |

|

|

|

|
 Izotoxal |

|

|

|

|
Note
- ↑ Format:En icon γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ↑ Format:En icon Octagram Calculator, rechneronline.de, accesat 2023-05-05
- ↑ Format:En icon The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum
Bibliografie
- Format:En icon Grünbaum, B. and G.C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), Format:Isbn
- Format:En icon Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70.
- Format:En icon John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, Format:Isbn (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)