Hexaedru tetrakis

În geometrie un hexaedru tetrakis este un poliedru Catalan cu 24 de fețe. Fiecare poliedru Catalan este dualul unui poliedru arhimedic. Dualul hexaedrului tetrakis este octaedrul trunchiat. Este tranzitiv pe fețe.
Poate fi considerat un cub cu piramide pătrate lipite pe fețele cubului, ca urmare este un Kleetop.
Ca dual al unui tetraedru omnitrunchiat poate fi considerat un hexaedru disdiakis sau tetraedru hexakis.
Coordonate carteziene și dimensiuni
Coordonatele carteziene ale celor 14 vârfuri ale unui hexaedru tetrakis centrat în origine, sunt punctele (±3/2, 0, 0), (0, ±3/2, 0), (0, 0, ±3/2) și (±1, ±1, ±1).
Lungimea laturilor scurte ale hexaedrului tetrakis este egală cu 3/2, iar cea a laturilor lungi este egală cu 2. Fețele sunt triunghiuri isoscele ascuțite. Unghiul mai mare din acestea este egal cu iar cele două mai mici sunt egale cu .
Dacă se notează lungimea laturii cubului de bază cu a, înălțimea apexului unei piramide de pe o față a cubului este Format:Sfrac. Înclinarea fețelor triunghiulare ale piramidei față de de fața cubului este arctg(Format:Sfrac), aproximativ 26,565°[1]. Baza triunghiului isoscel are lungimea a, iar celelalte două laturi au lungimea de Format:Sfrac, care se obține din teorema lui Pitagora aplicată înălțimii și semidiagonalei piramidei. Asta duce la o înălțime a triunghiului unei fețe de Format:Sfrac.[2] Aria triunghiului este Format:Sfrac, iar inghiurile interne sunt arccos(Format:Sfrac) (aproximativ 48,19°) iar unghiul complementar 180° − 2 arccos(Format:Sfrac) (aproximativ 83,62°).
Aria totală a hexaedrului triakis este suma ariilor fețelor, adică 3Format:Sqrta2.
Volumul unei piramide este Format:Sfrac; ca urmare volumul total al celor 6 piramide și a cubului central este Format:Sfrac.
Proiecții ortogonale
Hexaedrul tetrakis, dualul octaedrului trunchiat are 3 poziții de simetrie, două situate la vârfuri și una la mijlocul laturilor.
| Simetrie proiectivă |
[2] | [4] | [6] |
|---|---|---|---|
| Hexaedru tetrakis |
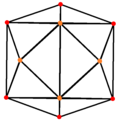
|

|
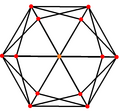
|
| Octaedru trunchiat |

|

|

|
Simetrie
Cu simetrie tetraedrică Td, [3,3] (*332), fețele triunghiulare reprezintă cele 24 de domenii fundamentale ale acestei simetrii. Acest poliedru poate fi construit din 6 cercuri mari pe o sferă. Poate fi considerat și un cub cu fețele pătrate triangulate prin vârfuri și centrele fețelor și un tetraedru cu fețele divizate de vârfuri, mijloacele laturilor și un punct central.

|

|

|

|

|
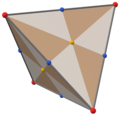
|
| Octaedru trunchiat |
Hexaedru disdiakis |
Dodecaedru rombic |
Hexaedru rombic |
Tetraedru | |
| Poliedru sferic | |||
|---|---|---|---|

|

|

|

|
| (animație) | Propiecții ortogonale după axele cu 2, 3 și 4 poziții | ||
Laturile hexaedrului tetrakis sferic sunt situate pe șase cercuri mari, care corespund planurilor de oglindire din simetria tetraedrică. Ele pot fi grupate în trei perechi de cercuri ortogonale (care se intersectează pe câte o axă de coordonate). În imaginile de mai jos, aceste hosoedre pătrate sunt colorate cu roșu, verde și albastru.
| Proiecții stereografice | |||
|---|---|---|---|

|
cu 2 poziții | cu 3 poziții | cu 4 poziții |

|

|

| |
Piramidă cubică
Este foarte asemănător cu desfășurata tridimensională a piramidei cubice cvadridimensionale, așa cum desfășurata unei piramide pătrate este un pătrat cu triunghiuri atașate pe fiecare latură a sa, desfășurata unei piramide cubice este un cub cu piramide pătrate atașate pe fiecare față a sa.
Poliedre și pavări înrudite
Format:Tabel figuri2 trunchiate
Acest poliedru face parte dintr-o secvență definită de configurația feței V4.6.2n. Acest grup este particular pentru că toți membrii săi au un număr par de laturi la vârf și formează plane care divid poliedrele și dreptele infinite din plan și continuând în planul hiperbolic pentru orice n ≥ 7.
Cu un număr par de fețe la fiecare vârf, aceste poliedre și pavări pot fi colorate alternativ cu numai două culori, astfel încât toate fețele adiacente să aibă culori diferite.
Fiecare față corespunde domeniul fundamental al unui grup de simetrie cu ordinul 2,3,n la fiecare vârf al feței triunghiulare. Format:Tabel omnitrunchiate
Note
Bibliografie
- Format:En icon Format:Cite book (Section 3-9)
- Format:En icon Format:Citation (The thirteen semiregular convex polyhedra and their duals, Page 14, Tetrakishexahedron)
- Format:En icon John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss (2008), The Symmetries of Things, Format:ISBN [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Tetrakis hexahedron)
Legături externe
- Format:En icon Format:Mathworld
- Format:En icon Format:Mathworld
- Format:En icon Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
- Format:En icon Model VRML Format:Webarchive
- Format:En icon Conway Notation for Polyhedra Chei: "dtO" sau "kC"
- Format:En icon Tetrakis Hexahedron – Interactive Polyhedron model
- Format:En icon The Uniform Polyhedra