Teorema lui Menelaus

Cazul 1: Dreapta DEF trece prin triunghiul ABC

Cazul 2: Dreapta DEF nu trece prin triunghiul ABC

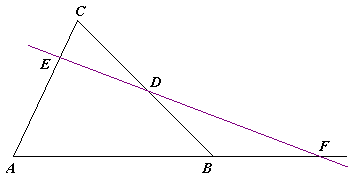
Teorema lui Menelaus este una din teoremele clasice ale geometriei. Poartă numele lui Menelau din Alexandria, căruia îi este atribuită. Se referă la intersecția laturilor unui triunghi cu o dreaptă.

Definiție

Dacă punctele $D,E$ și $F$ sunt conținute, respectiv, în dreptele $BC,CA$ și $AB$ ale triunghiului $\mathrm{△}ABC$, rezultă că ele sunt coliniare dacă și numai dacă are loc relația:

$\frac{AE}{EC}\cdot \frac{CD}{DB}\cdot \frac{BF}{AF}=1.$

Teorema reciprocă

Dacă D aparține lui BC, E aparține lui CA, F aparține lui AB și dacă D, E, F sunt situate două pe laturi și unul pe prelungirea laturii sau toate trei pe prelungirile laturilor și dacă

$\frac{DB}{DC}\cdot \frac{EC}{EA}\cdot \frac{FA}{FB}=1$, atunci punctele $D,E,F$ sunt coliniare.

Vezi și

• Teorema lui Ceva